Program verification and testing

Correctness

When is a program correct?

When it fulfills its specification
What is a specification?

To state explicitly or in detail what a program should do!
How to establish a relation between the specification and the implementation?
What about bugs in the specification?

We need to trust our specification.

In this lecture

We cover to (quite different) techniques to show that an implementation adheres to its specification

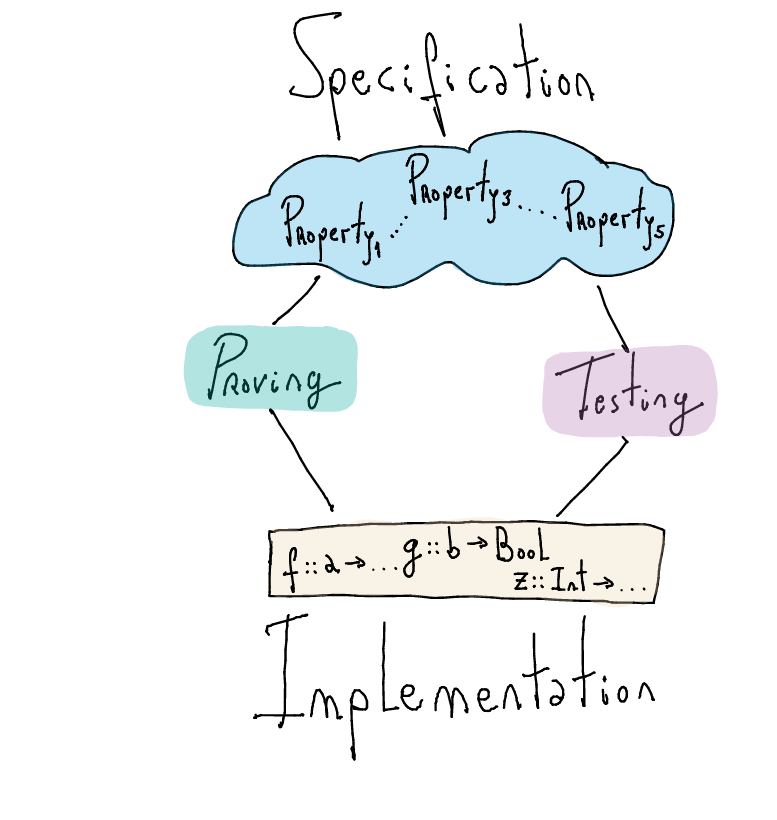
Proving: equational reasoning
Testing: property-based testing

Equational reasoning

We know that Haskell supports equational reasoning, i.e., changing equals by equals
Referential transparency is key!

Example: insertion sort

Length of lists

 length :: [a] -> Int
 length []       = 0
 length (x : xs) = 1 + length xs

Inserting an element in an ordered list

insert :: Ord a => a -> [a] -> [a]
insert x [] = [x]
insert x (y : ys)
         | x <= y    = x : y : ys
         | otherwise = y : insert x ys

Insertion sort

isort :: Ord a => [a] -> [a]
isort []       = []
isort (x : xs) = insert x (isort xs)

Proving correctness of `isort`

We can capture the "right" behavior of isort with many properties
We consider that the length of a sorted list is the same as the list before being sorted.
```
length (isort xs) == length xs 
```
for any finite and well-defined list xs
How do we prove it?

Properties regarding data types can often be proved by induction
To prove that
```
P xs
```
holds for a given property P and list xs, it is enough to prove that
- Base case:
```
P [] 
```
  holds.
- Inductive case:
  
  Assuming that
```
P xs 
```
  holds for any xs, then it must hold
```
P (x:xs) 
```
  for any x
We try to prove
```
length (isort xs) == length xs 
```
by induction
- Base case:
```
length (isort []) =?= length [] 
```
  Symbol =?= is used to indicate uncertainty about the equality. In other words, length (isort []) =?= length [] indicates that we are not sure if the equality holds. After all, that is what we should prove!
```
    length (isort [])
== {definition isort.0}
    length []
== {definition length.0}
    0
== {definition length.0}
    length [] 
```
  So, we complete the proof for the base case.
- Inductive case:
  
  This is often the most interesting case. We assume that
```
length (isort xs) == length xs 
```
  and we should show that
```
length (isort (x:xs)) =?= length (x:xs) 
```
  So, we start trying to unfold definitions.
```
     length (isort (x:xs))
 == {definition isort.1)
     length (insert x (isort xs)) 
```
  At this point, to continue unfolding the expression, we need to do case analysis on xs, i.e., xs == [] and xs == y:ys.
  
  *Deconstructing the inductive argument is not always a good idea*. It might be an indication that we need to think about an auxiliary lemma(s).

Auxiliary lemmas

If we see the expression where we got stuck
```
length (insert x (isort xs)) 
```
What can we know about it? Can it be generalized?

Generalization is *very* important to simplify expressions and make proofs simpler

We can generalize the expression

length (insert x (isort xs))

to be

length (insert x ys)

What can we say about that?

We would like to show that

length (insert x ys) == 1 + length ys

How can we prove it? By induction!

Base case:

    length (insert x [])
== {definition insert.0}
    length [x]
== {definition length.1}
    1 + length []

Inductive case:

We assume that

length (insert x ys) == 1 + length ys

and we should prove that

length (insert x (y:ys)) == 1 + length (y:ys)

Thus, we take

length (insert x (y:ys))

and unfold definitions.

Case x <= y:

     length (insert x (y:ys))
 == {definition insert.1}
     length (x:y:ys)
 == {definition length.1}
     1 + length (y:ys)

Case otherwise:

    length (insert x (y:ys))
== {definition insert.1}
    length (y : insert x ys)
== {definition length.1}
    1 + length (insert x ys)
== {inductive hypothesis!)
    1 + (1 + length ys)
== {definition length.1}
    1 + length (y:ys)

Proving `isort` with auxiliary lemma

We were stuck in the inductive case of

length (isort (x:xs)) =?= length (x:xs)

To prove this, as before, we assume

length (isort xs) == length xs

and we unfold the expression length (isort (x:xs)).

     length (isort (x:xs))
 == { definition isort.1 }
     length (insert x (isort xs))
 == {by auxiliary lemma taking ys == (isort xs) }
     1 + length (isort xs)
 == {by induction hypothesis}
     1 + length (xs)
 == { definition length.1 }
     length (x:xs)

The proof goes through!

It is often the case that auxiliary lemma(s) are needed in order to complete the proof
Proof skeleton

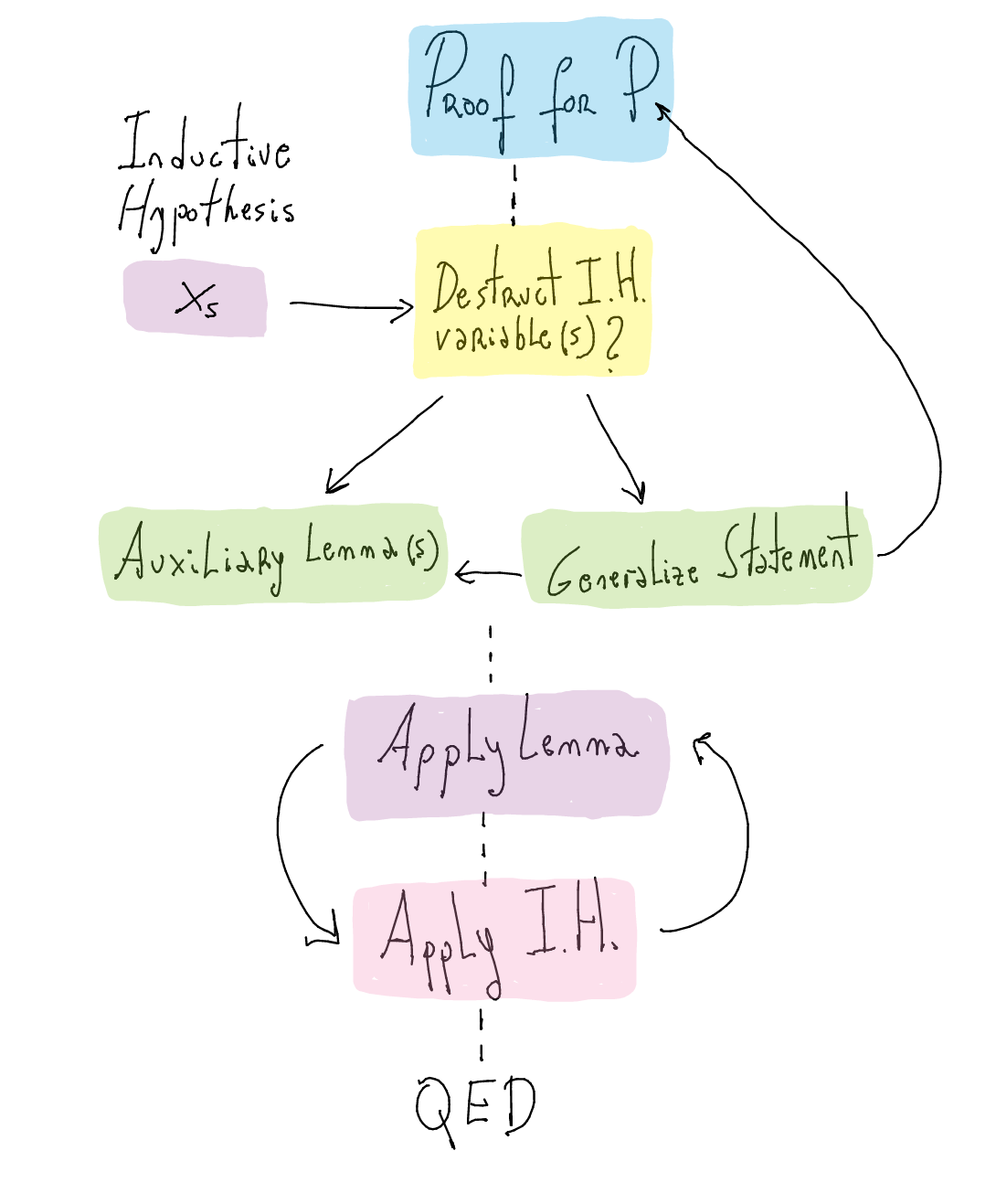
When doing a proof, it is often the case that, in order to make some progress, it is necessary to destruct a variable which is part of the inductive hypothesis (IH). This situation might be a hint that we need to either generalize the theorem statement or to prove auxiliary lemmas. Bear in mind that auxiliary lemmas' statements might be a generalization of what the proof needs (see next example below). To finish the proof, we then proceed to apply the auxiliary lemmas first and then the IH or vice versa.

Proving more properties

Consider the function

reverse :: [a] -> [a]
reverse []     = []
reverse (x:xs) = reverse xs ++ [x]

How do we know if the function is correct?

We can start by lining up several properties that it must fulfill

length (reverse xs)  == length xs
reverse (reverse xs) == xs
...

Let us try to prove
```
reverse (reverse xs) == xs 
```
We proceed by induction on the list structure.
- Base case:
```
    reverse (reverse [])
== {definition reverse.0}
    reverse []
== {definition reverse.0}
    [] 
```
- Inductive case:
  
  We assume that
```
reverse (reverse xs) == xs 
```
  and we need to prove that
```
reverse (reverse (x:xs)) =?= (x:xs) 
```
  So, we have that
```
    reverse (reverse (x:xs))
== {definition reverse.1}
    reverse (reverse xs ++ [x]) 
```
  At this point, in order to proceed, we need to destruct the inductive variable xs. As before, this situation is an indication that we need to think about an auxiliary lemma or generalize the theorem statement.
  
  Let us scrutinize where we got stuck.
```
reverse (reverse xs ++ [x]) 
```
  What can we say about this expression? It is quite complicated. Let us generalize it in order to simplify it!
```
reverse (ys ++ zs) 
```
  Observe that if we make ys == reverse xs and zs == [x], we obtain the expression where we got stuck in the proof.
  
  What can we say about this expression?
```
reverse (ys ++ zs) =?= reverse zs ++ reverse ys 
```
  The reverse of two concatenated lists is the concatenation of their reverse! This is going to be our auxiliary lemma.

Auxiliary lemma for `reverse`

We are going to assume some properties about concat
```
xs ++ [] == xs
(xs ++ ys) ++ zs == xs ++ (ys ++ zs)
```
Exercise: prove the properties of `(++)` described above

We proof by induction on ys

reverse (ys ++ zs) == reverse zs ++ reverse ys

Base case:

    reverse ([] ++ zs)
== {definition (++)}
    reverse zs
== {property of (++)}
    reverse zs ++ []
== {definition reverse.0}
    reverse zs ++ reverse []

Inductive case:

We assume that

reverse (ys ++ zs) == reverse zs ++ reverse ys

and we need to prove that

reverse ((y:ys) ++ zs) == reverse zs ++ reverse (y:ys)

    reverse ((y:ys) ++ zs)
== {definition (++)}
    reverse (y:(ys ++ zs))
== {definition of reverse.1 with x == y, xs == ys ++ zs}
    reverse (ys ++ zs) ++ [y]
== {inductive hypothesis}
    (reverse zs ++ reverse ys) ++ [y]
== {associativity of (++)}
    reverse zs ++ (reverse ys ++ [y])
== {definition of reverse.1}
    reverse zs ++ reverse (y:ys)

Proving `reverse` with auxiliary lemma

We come back to the case where we got stuck

 reverse (reverse (x:xs)) =?= (x:xs)

So, we have that

     reverse (reverse (x:xs))
 == {definition reverse.1}
     reverse (reverse xs ++ [x])
 == {by auxiliary lemma with ys == reverse xs, zs == [x]
     reverse [x] ++ reverse (reverse xs)
 == {by inductive hypothesis}
     reverse [x] ++ xs
 == {definition of reverse.1}
     ([] ++ [x]) ++ xs
 == {definition (++)}
     [x] ++ xs
 == {definition of (:)}
     x:[] ++ xs
 == {definition of (++)}
     x:([] ++ xs)
 == {definition of (++)}
     (x:xs)

The proof now goes through!

Equational reasoning summary

Equational reasoning can be an elegant way to prove properties of a program
Equational reasoning can be used to establish a relation between an obviously correct Haskell program (a specification) and an efficient Haskell program
Equational reasoning is usually quite lengthy
Careful with special cases (laziness):
- undefined values;
- infinite values
It is not feasible to prove properties about every Haskell program using equational reasoning
Other proof methods
- Proof assistants: Agda, Coq, Isabelle, etc.
- It provides mechanized proofs and opens the door for proof-scalability (next lecture!)

Property-based testing

Rather than formally proving that a program is correct, we are going to test it against its specification
Importantly, the test cases are generated automatically
We will use QuickCheck, a Haskell library developed at Chalmers by Koen Claessen and John Hughes
QuickCheck is essentially an embedded domain-specific language (EDSL) for defining properties and test implementations against them
- Automatic datatype-driven generation of random test data, i.e., QuickCheck uses the type information of your data to generate test cases!
- Users can extend the generation of random test data to fit their needs
- Shrinks failing test cases

For the rest of the lecture, we play with QuickCheck code (see repository)