Monad transformers II: composition of error and state transformers

The except (error) monad transformer

In our interpreter, expressions might refer to unbound variables / references.
```
> runEval $ eval $ parse "q + 1"
*** Exception: Variable q not found.
```
```
> runEval $ eval $ parse "!q"
*** Exception: Variable q not found.
```
We need some exception handling mechanism into the language of expressions.
We add a data type which captures the type of exceptions (errors) occurring in our interpreter:
```
data Err = SegmentationFault
         | UnboundVariable String
         | OtherError String
```

First, we could explicitly indicate that errors might happen in the interpreter
```
eval :: Expr -> Either Err Value
```
This means that there would be some plumbing to check if every recursive call has finished succesfully, and if it is not the case, fail the whole computation.
Instead we use a monad transformer!

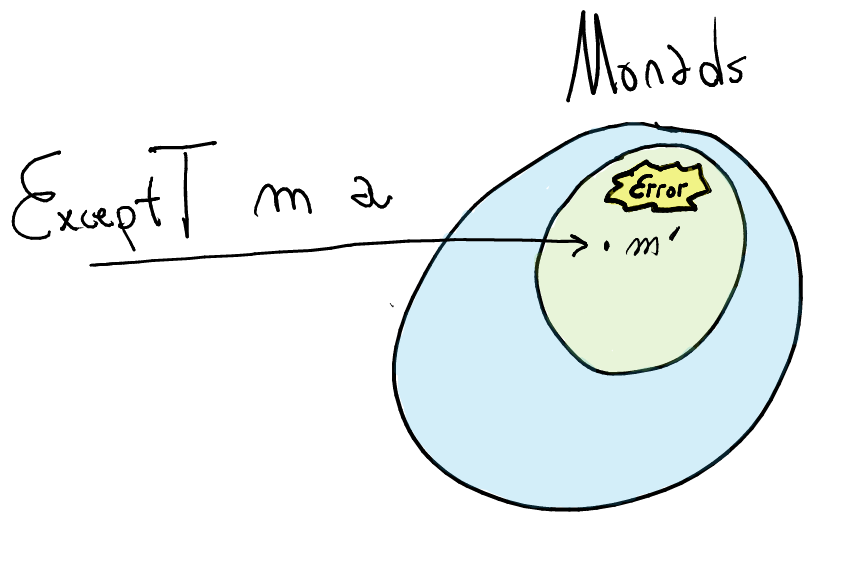
ExceptT takes a monad m and returns a monad which support two operations: throwError and catchError — such monads are called MonadError.

A monad obtained by the transformer `ExceptT` is a `MonadError`!
```
  type ExceptT e m a

  runExceptT :: ExceptT e m a -> m (Either e a)

  throwError :: MonadError e m => e -> m a
  catchError :: MonadError e m => m a -> (e -> m a) -> m a
```

Composition of effects

We add an error monad (called exception monad in GHC) to our evaluation monad Eval.
We can understand the interaction between the state monad and the error monad by looking at their implementations (i.e. types).
It matters whether we stick the error monad on the outside or the inside of the state monad.
With ExceptT on the outside, we will represent computations as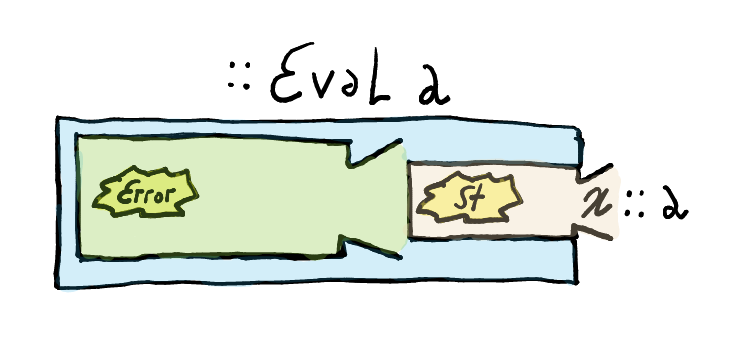

We have computations of type
```
  ExceptT err (State s) a
```
which is isomorphic to:
```
  State s (Either err a)
```
which is in turn isomorphic to:
```
  s -> (Either err a, s)
```
No matter whether we return Right a or Left err, the final state is also returned.

State changes will not be rolled back when there's an exception.

When there is an exception, the state information is there!

Instead, if we place ExceptT on the inside, i.e., adding a state monad on top of an error monad, computations will be represented as: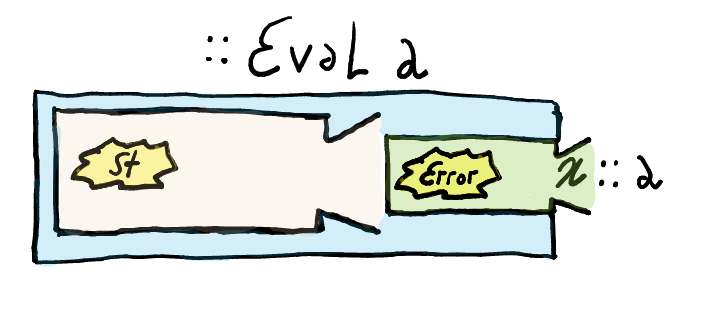

We will have computations of the type
```
  StateT s (Except e) a
```
which is isomorphic to
```
  s -> Except e (a, s)
```
and in turn
```
  s -> Either e (a, s)
```
If a computation fails, we lose any changes to the state made by the failing computation.

Observe that the state is just passed as a return value in the underlying monad.

Interpreter 3: `ExceptT` on the inside

code

We apply the monad transformer on the inside and wrap it with a reader and state monad.

  newtype Eval a = Eval
    { unEval ::
        StateT Store
               (ReaderT Env
                        (ExceptT Err Identity)) -- new
               a
    } deriving
      ( Functor, Applicative, Monad
      , MonadState  Store
      , MonadReader Env
      , MonadError  Err -- new
      )

The run function then includes runExceptT right after the reader's run function

  runEval :: Eval a -> Either Err a     -- new type!
  runEval m = m
    & unEval
    & (`evalStateT` emptyStore)
    & (`runReaderT` emptyEnv)
    & runExceptT
    & runIdentity

We adapt the interpreter's auxiliary functions such that they can raise errors:

Looking up a variable in the environment

  lookupVar :: Name -> Eval Value
  lookupVar x = do
    env <- ask
    case Map.lookup x env of
      Nothing -> throwError (UnboundVariable x) -- new
      ...

Deferencing a location which does not exist

  deref :: Ptr -> Eval Value
  deref p = do
    st <- get
    let h = heap st
    case Map.lookup p h of
      Nothing -> throwError SegmentationFault -- new
      ...

We finally write our interpreter (the only new case is Catch)

  eval :: Expr -> Eval Value
  eval (Lit n)       = return n
  eval (a :+: b)     = (+) <$> eval a <*> eval b
  eval (Var x)       = lookupVar x
  eval (Let n e1 e2) = do v <- eval e1
                          localScope n v (eval e2)
  eval (NewRef e)    = do v <- eval e
                          newRef v
  eval (Deref e)     = do r <- eval e
                          deref r
  eval (pe := ve)    = do p <- eval pe
                          v <- eval ve
                          p =: v
  eval (Catch e1 e2) = catchError (eval e1) (\ _err -> eval e2)

We can recover from errors

  testExpr2 = parse "(try !p catch 22) + 1738"

  >>> runEval $ eval testExpr2
  1760

What happens with the side-effects when an error occurs?

  testExpr3 = parse
    "let one = new 1; \
    \ let dummy = (try ((one := 2) + !7) catch 0); \
    \ !one"

What is the value of one?

Let us run it first
```
  >>> runEval $ eval testExpr3
  Right 1
```
The side-effects (namely, one := 2) are reverted if an error occurs!
To explain what happens in more detail, let us see the program

The expression ((one := 2) + !7) can be thought as a function which takes a store and always returns an error, i.e. a function semantically equivalent to \ s -> Left SegmentationFault.

Then, due to the try-catch statement, the expression (try ((one := 2) + !7) catch 0) catches the error and then produces a function semantically equivalent to \ s -> Right (Lit 0, s). Observe that it returns the state before the effect one := 2.

Interpreter 4: `ExceptT` on the outside

code

We apply the exceptionmonad transformer on the outside:

  newtype Eval a = Eval
    { unEval ::
        ExceptT Err                              -- new
                (StateT Store
                        (ReaderT Env Identity))
                a
    } deriving
      ( Functor, Applicative, Monad
      , MonadState  Store
      , MonadReader Env
      , MonadError  Err -- new
      )

Since ExceptT is the outermost transformer, runExceptT is the first one to run

  runEval m = m
    & unEval
    & runExceptT
    & (`evalStateT` emptyStore)
    & (`runReaderT` emptyEnv)
    & runIdentity

The interpreter, and the auxiliary functions remain the same.
What happens with the side-effects when an error occurs?
```
  testExpr3 = parse
    "let one = new 1; \
    \ let dummy = (try ((one := 2) + !7) catch 0); \
    \ !one"
```
What is the value of one?
```
  >>> runEval $ eval testExpr3
  Right 2
```
Observe that the program has recovered but the side-effects within the try-catch blocked were not rolled-back.
To explain what happens in more detail, let us see the program:

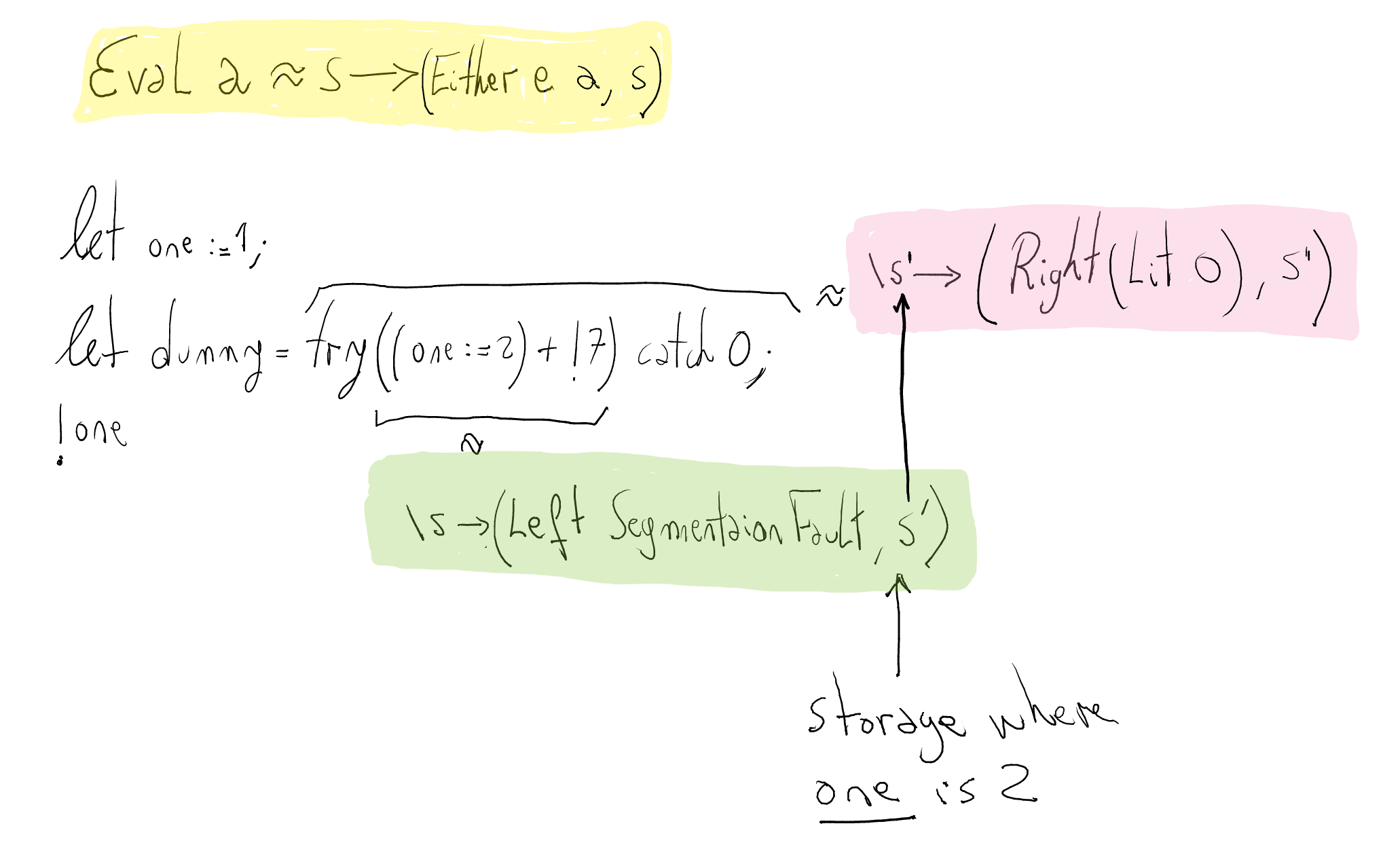
The expression ((one := 2) + !7) can be thought as a function which takes a store and returns an error but keeping the state at the point of the failure. You can think of the computation as a function semantically similar to \ s -> (Left SegmentationFault, s') where s' is the same store as s except that reference one is set to 2.

When the exception handler is executed, it takes the state from where ((one := 2 + !7)) left it, i.e. s'. So, the result of !one in the last line of the program is 2.

Which one is better? ExceptT outside or inside?

That is application-specific.
In our interpreter, the expected semantics for programs is obtained with ExceptT on the inside.
There are some side-effects which cannot be undone, e.g., launching a missile. For those effects, ExceptT on the outside might be suitable.

Interpreter 5: Adding I/O

code

We want to add a new effect: I/O (for simplicity we only consider output).
We will add a function to print out messages:
```
  let x = print \"hello\" ; 42
```

We will add the IO monad into the definition of Eval

  newtype Eval a = Eval
    { unEval ::
        StateT Store
               (ReaderT Env
                        (ExceptT Err IO)) -- new IO for Identity
               a
    } deriving
      ( Functor, Applicative, Monad
      , MonadState  Store
      , MonadReader Env
      , MonadError  Err
      , MonadIO -- new
      )

We replaced Identity by IO.

The type Eval a is isomorphic to:
```
  s -> r -> Either Err (IO (a, s))
```
This indicates that the except (error) monad still rolls back the effects on the store, but not the ones in IO (e.g., launch a missile).
We make Eval an instance of the class MonadIO.

As a result, Eval can lift (cast) every IO-action into itself:
```
  liftIO :: MonadIO m => IO a -> m a
```

We define the function to show a string:

  msg :: String -> Eval ()
  msg = liftIO . putStrLn

We add a constructor to represent output commands:

  eval :: Expr -> Eval Value
  eval (Lit n)       = return n
  eval (a :+: b)     = (+) <$> eval a <*> eval b
  eval (Var x)       = lookupVar x
  eval (Let n e1 e2) = do v <- eval e1
                          localScope n v (eval e2)
  eval (NewRef e)    = do v <- eval e
                          newRef v
  eval (Deref e)     = do r <- eval e
                          deref r
  eval (pe := ve)    = do p <- eval pe
                          v <- eval ve
                          p =: v
  eval (Catch e1 e2) = eval e1 `catchError` \ _err -> eval e2
  eval (Print m)     = do msg m  -- new
                          return 0

The following program produces an I/O effect before an exception is thrown
```
   "let one = new 1; \
  \ let dummy = (try ( print \"hello!\" + (one := 2) + !7) \
  \             catch 0); \
  \ !one"
```
If we run it, it produces the output and then it rolls back the effects on the store (i.e., one := 2):
```
  >>> test3
  hello!
  Right 1
```

Implementing monad transformers

So far, we have just seen how to use the monad transformers provided by GHC and the magic of deriving.
In case you designed your own monad to handle certain special effects, you might want to make a monad transformer for adding such effects to any monad!
We will develop the state, error, and reader monad transformers.

`MyStateT`: a state monad transformer

We start by defining a data type to host the transformed monad, i.e., the monad which the transformer considers.
```
  data MyStateT s m a
```
The transformer takes the monad m and synthesises a new monad with state (of type s) which contains m underneath.
To write a monad transformer, it is usually a good principle to see the underlying monad as a black-box, i.e., you should assume nothing about its structure.
If monad m is black-box, you can only use its return, (>>=), and the non-proper morphisms
Importanty, recall that monad m is polymorphic on the produced result, e.g., you could have monadic computations of type m Int, m Char, m [Int], etc.
Inside the implementation of MyStateT, we will exploit the polymorphism of m to choose a convenient type for the result which helps to implement the new monad
Let us see now a possible implementation of MyStateT
```
  newtype MyStateT s m a = MyStateT { runMyStateT :: s -> m (a,s) }
```
The state monad transformer models computations as a function which takes a state (of type s) and returns a computation m (the underlying monad).

Importantly, the computation m produces a result (of type a) and the resulting state (of type s).

Observe how the state monad transformer uses m to keep track of the resulting state by simply instantiating the type m's result to be (a, s).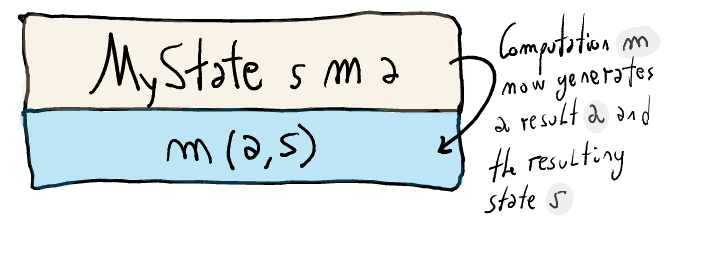
Given the implementation of MyStateT, we now show that MyStateT s m a is a monad for every underlying monad m.

When defining return and (>>=) for MyStateT, we are going to use return and (>>=) given for m — recall that we should see m as black-box!
```
  return x = MyStateT \ s  -> return (x, s)
```
Observe that return for MyStateT uses return (x,s) :: m (a, s).

For the bind, we start by indicating that the result of the bind is a monadic value from our monad transformer. Therefore, we know that
```
   MyStateT f >>= k = MyStateT \ s1  -> ...
```
We are going to use the types to guide us in completing the definitions.

We know that k :: a -> MyStateT s m b is waiting for a value of type a, and we have the statefull computation f :: s -> m (a,s) which produces an a when given a state of type s. We have state s1 :: s in scope, let's use it!
```
  MyStateT f >>= k = MyStateT \ s1 -> do
    (a, s2) <- f s1
    ... (k a) ...
```
Observe that (k a) :: MyStateT s m b, but the type for the whole missing code must be ... (k a) ... :: m (b, s). As a first step, we can destruct MyStateT and obtain its underlying computation of type s -> m (b, s).
```
  MyStateT f >>= k = MyStateT \ s1  -> do
    (a, s2) <- f s1
    runMyStateT (k a) ...
```
Still, the type for runMyStateT (k a) :: s -> m (b, s), i.e., we need to provide a state of type s to obtain a term of type m (b, s). At this point, we have two states in scope: s1 and s2. Which one should we use? Since MyStateT s m a is a state monad, it should "pass along" the state between subcomputations. Thus, we will pass the resulting state after running f s1, i.e., s2.
```
  MyStateT f >>= k = MyStateT \ s1 -> do
    (a, s2) <- f s1
    runMyStateT (k a) s2
```
Now that MyStateT s m is a monad (do not forget to prove the monadic laws), we also need to provide the non-proper morphisms get and put corresponding to state monads:
```
  instance Monad m => MonadState s (MyStateT s m) where
    get   = MyStateT \ s -> return (s, s)
    put s = MyStateT \ _ -> return ((),s)
```

We leave it as an exercise to define the run functions

  evalMyStateT :: Monad m => MyStateT s m a -> s -> m a
  runMyStateT  :: Monad m => MyStateT s m a -> s -> m (a, s)

Monad transformers: lifting non-proper morphisms

So far, we have shown how MyStateT s m a takes a monad m and synthesizes a state monad with m underneath.

For that, we show how return and (>>=) for MyStateT can be defined based on return and (>>=) for monad m.
What about the non-proper morphisms of m? Can we reuse them in MyStateT s m?
A monad transformer is also responsible to provide the tools to take a non-proper morphism in m and lift it to work in MyStateT s m.
We declare a type-class for monad transformers, which contains a method for lifting operations from the underlying monad:
```
  class Monad m => MT m mT | mT -> m where
    lift :: m a -> mT a
```
This type class denotes that mT is a monad transformer which takes m as its underlined monad.

The type for lift takes a monadic operation in m (of type m a) and returns a computation that works in mT instead (of type mT a).

We show that MyStateT is a monad transformer:

  instance Monad m => MT m (MyStateT s m) where
     lift m = MyStateT \ s -> do
       a <- m
       return (a, s)

Observe that lift only runs the computation m without changing the state.

`MyExceptT`: an error monad transformer

As before, we start by defining a data type to host the transformed monad, i.e., the monad which the transformer considers.
```
  data MyExceptT e m a
```
To implement MyExceptT e m a, we need to add a mechanism to track if a computation has successfully or erroneously produced a value.

We will exploit the polymorphism of m to instantiate the type of the result with a data type which can keep track of errors.
```
  data MyExceptT e m a = MyExceptT { runMyExceptT :: m (Either e a) }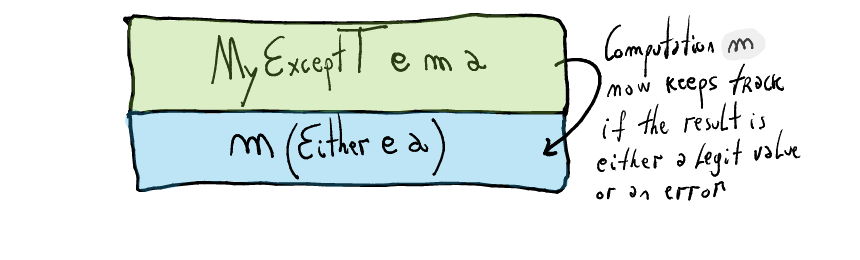
```

We define MyExceptT e m as a monad

As before, to define return and (>>=) for MyExceptT e m, we are to use return and (>>=) for the underling monad m

The return function for MyExceptT e m returns a successful computation, i.e., a value of the form Right x for some x.
```
  return a = MyExceptT $ return $ Right a
```
Observe the use of return from the underlying monad m, where return (Right a) :: m (Either e a).

To define m >>= k for MyExceptT e m, the bind must check that if the computation m fails, then m >>= k must also fail — thus, propagating the error. Otherwise, the bind must give the result of m to k and run the subsequent computation. With this in mind, we start defining the bind for MyExceptT e m.
```
  MyExceptT m >>= k = MyExceptT ...
```
The bind needs to check if the computation m produces a value or an error. To observe the value that m produces, we have no other choice than to run it and extract the resulting value — recall that we consider m as a black-box. For that, we use the (>>=) from the underlying monad.
```
  MyExceptT m >>= k = MyExceptT $
    m >>= \ result -> ...
```
We capture what m produces in the variable result. Then, we inspect it to see if it is a legit value or an error.
```
  MyExceptT m >>= k = MyExceptT $
    m >>= \ result -> case resullt of
      ...
```
If result is an error, i.e., a value of the form Left e, we propagate it.
```
  MyExceptT m  >>= k = MyExceptT $
    m >>= \case
      Left e -> return (Left e)
      ...
```
Observe that return (Left e) :: m (Either e a). In case that result is of the form Right a, i.e., a legit value, the bind needs to continue running the computation as indicating by k — for that, we need to give it the value produced by m.
```
  MyExceptT m  >>= k = MyExceptT $
    m >>= \case
      Left e  -> return (Left e)
      Right a -> ... k a ...
```
Observe, however, that k a :: MyExceptT e m b while we need an expression of type m (Either e b), which is contained in k a. Thus, we extract it by simply applying runMyExceptT.
```
MyExceptT m >>= k = MyExceptT $
  m >>= \case
    Left e  -> return (Left e)
    Right a -> runMyExceptT (k a)
```
Now that MyExceptT e m is a monad (again, do not forget to prove the monadic laws), we need to provide the non-proper morphisms throwError and catchError for error monads.
```
  throwError e = MyExceptT $ return (Left e)
```
Observe that return (Left e) :: m (Either e a). To define catchError, we need to observe if the computation passed as first argument produces a legit value or an error.
```
  catchError (MyExceptT m) h = MyExceptT $ ...
```
Computation m is given in the underlying monad. Therefore, to observe the value produced by m, we need to run it and extract its result with the (>>=) from the underlying monad.
```
   catchError (MyExceptT m) h = MyExceptT $
     m >>= \ result -> ...
 
```
We then need to inspect the shape of result. In case that result is of the form Right a (for some value a), catchError does not need to engage the exception handler, but rather return this value.
```
   catchError (MyExceptT m) h = MyExceptT $
     m >>= \case
       Right a -> return (Right a)
       ...
 
```
If m instead produces an error, catchError needs to engage the exception handler.
```
   catchError (MyExceptT m) h = MyExceptT $
      m >>= \case
        Right a -> return (Right a)
        Left  e -> ... (h e) ...
 
```
We have the type for (h e) :: MyExceptT e m a, but we need an expression of type m (Either e a) for the code ... (h e) .... For that, we deconstruct h e by using runMyExceptT.
```
   catchError (MyExceptT m) h = MyExceptT $
      m >>= \case
        Right a -> return (Right a)
        Left  e -> runMyExceptT (h e)
 
```

We leave it as an exercise to define the run function

  runMyExceptT :: MyExceptT e m a -> m (Either e a)

We show that MyExceptT e is a monad transformer by providing a lifting operation
```
  instance Monad m => MT m (MyExceptT e m) where
    lift m = MyExceptT $ m >>= \ a -> return (Right a)
```
The lift function simply runs the computation m from the underlying monad and wraps its result with a Right constructor.

`MyReaderT`: a reader monad transformer

We start by defining a data type to host the transformed monad, i.e., the monad which the transformer considers.
```
  type MyReaderT r m a
```
To implement MyReaderT r m a, we need to add a mechanism to provide a computation m a with some environment (read-only state).
```
  newtype MyReaderT r m a = MyReaderT { runMyReaderT :: r -> m a}
```
For that, we make m a depend on an environment of type r.

**Exercise**: Define `MyReaderT r m` as a monad, i.e, implement `return` and `(>>=)`.

**Exercise**: Show that `MyReaderT r m` is a reader monad, i.e., implement functions `ask` and `local`.

**Exercise**: Show that `MyReaderT r m` is a monad transformer, i.e., implement the `lift` function.

Interpreter 6: an interpreter with `MyStateT`, `MyExceptT`, and `MyReaderT`

code

We define the monad stack using our own monad transformers

type Eval a = (MyStateT Store
                        (MyReaderT Env
                                (MyExceptT Err Identity))
                        a )

We can see our monad stack graphically as follows

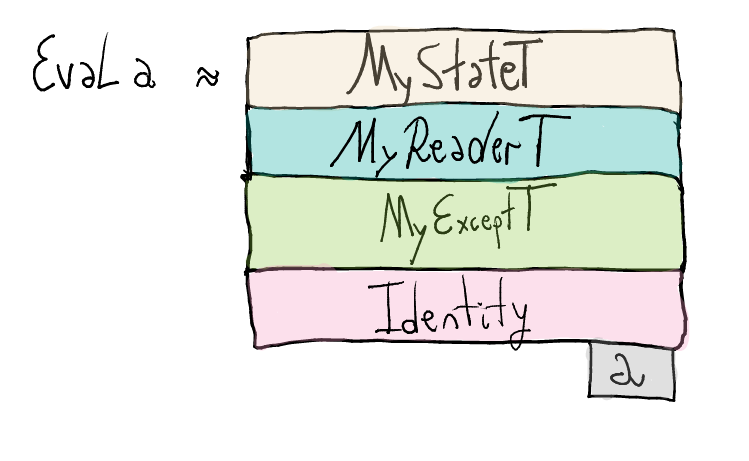
We adapt the run function accordingly

runEval :: Eval a -> Either Err a
runEval m = m
  & (`evalMyStateT` emptyStore)
  & (`runMyReaderT` emptyEnv)
  & runMyExceptT
  & runIdentity

To run a computation of type Eval a, we need to run the whole monad stack.

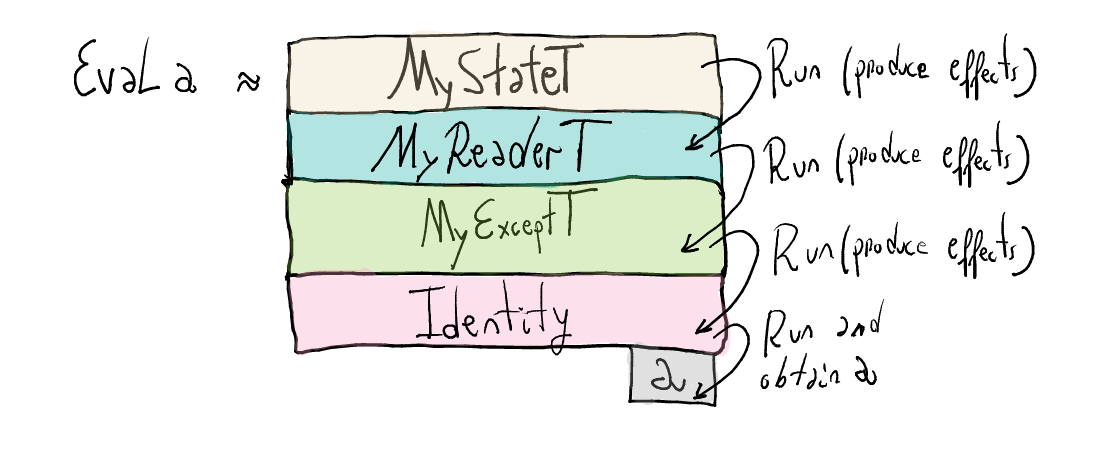
Lifting operations I

When introducing the new definition for Eval in the code for Interpreter 4, there are some auxiliary functions which do not type check.
We start by focusing on the auxiliary function lookupVar:
```
  lookupVar :: Name -> Eval Value
  lookupVar x = do
    env <- ask
    case Map.lookup x env of
      Nothing -> throwError (UnboundVariable x)
      Just v  -> return v
```
This code now does not type check for two reasons.

Firstly, the ask function has type MyReaderT Env (MyExceptT Err Identity) a, while the lookupVar is defined for the whole stack, i.e, a monad of type MyStateT Store (MyReaderT Env (MyExceptT Err Identity)).

Graphically, we have an operation in one for the layers of the monad stack and we want to make it work for the whole stack.

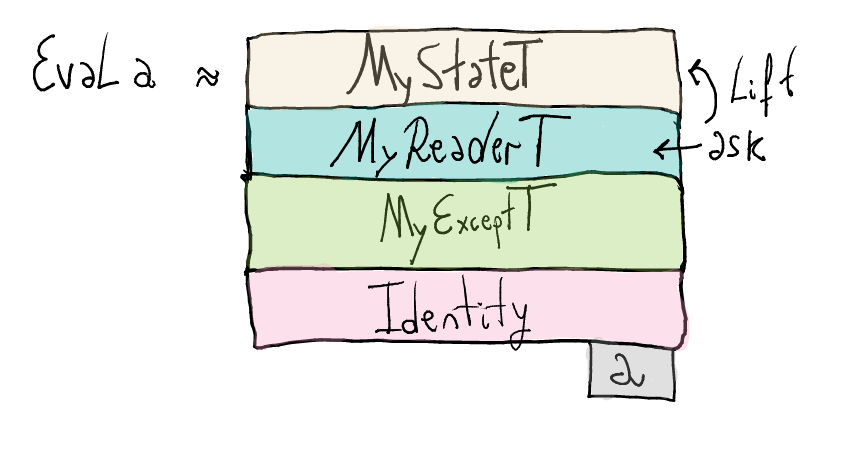
We then lift ask to work with the top-level layer (MyStateT).
```
  lookupVar x = do
    env <- lift ask -- new
    case Map.lookup x env of
      Nothing -> throwError (UnboundVariable x)
      Just v  -> return v
 
```
Secondly, throwError has type MyExceptT Err Identity a, while lookupVar is defined for whole monad stack.

As before, we have an operation in one of the layers of the monad stack and we want to make it work for the whole stack. In this case, however, we need to lift it two layers up.

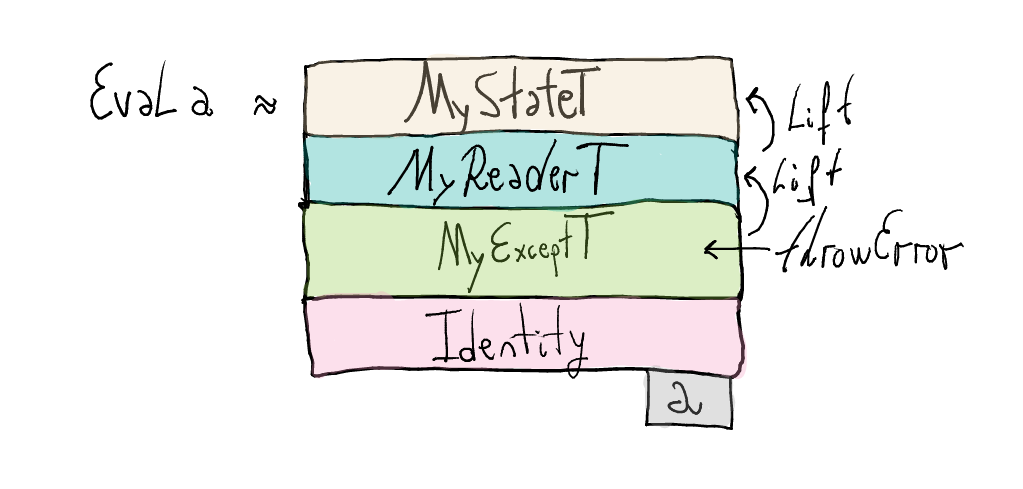
In the code, function lift is applied twice.
```
 lookupVar :: Name -> Eval Value
 lookupVar x = do
   env <- lift ask
   case Map.lookup x env of
     Nothing -> lift (lift (throwError (UnboundVariable x))) -- new
     Just v  -> return v
```
The definition for lookupVar above type-checks.
Similar to lookupVar, auxiliary function localScope does not type check and needs to be changed. However, the reason why it does not work cannot be simply fixed by calling function lift (explained below).

Lifting operations II

It is not always as easy as applying lift in order to use a non-proper morphism from the underlying layers
To illustrate this point, we will examine the code for the constructor Catch.

In the interpreter 4, the code was
```
eval (Catch e1 e2) = catchError (eval e1) (\ _err -> eval e2)
```
However, this line of code does not type check if we use our own monad transformers.

The reason for that is that
```
  eval e1 :: Eval a
  \ _err -> eval e2 :: Err -> Eval a
```
and function catchError is working at the layer introduced by MyExceptT. Because of that, catchError expects two arguments, let's called it arg1 and arg2, with the following types
```
  arg1 :: MyExceptT Err Identity a
  arg2 :: e -> MyExceptT Err Identity a
```
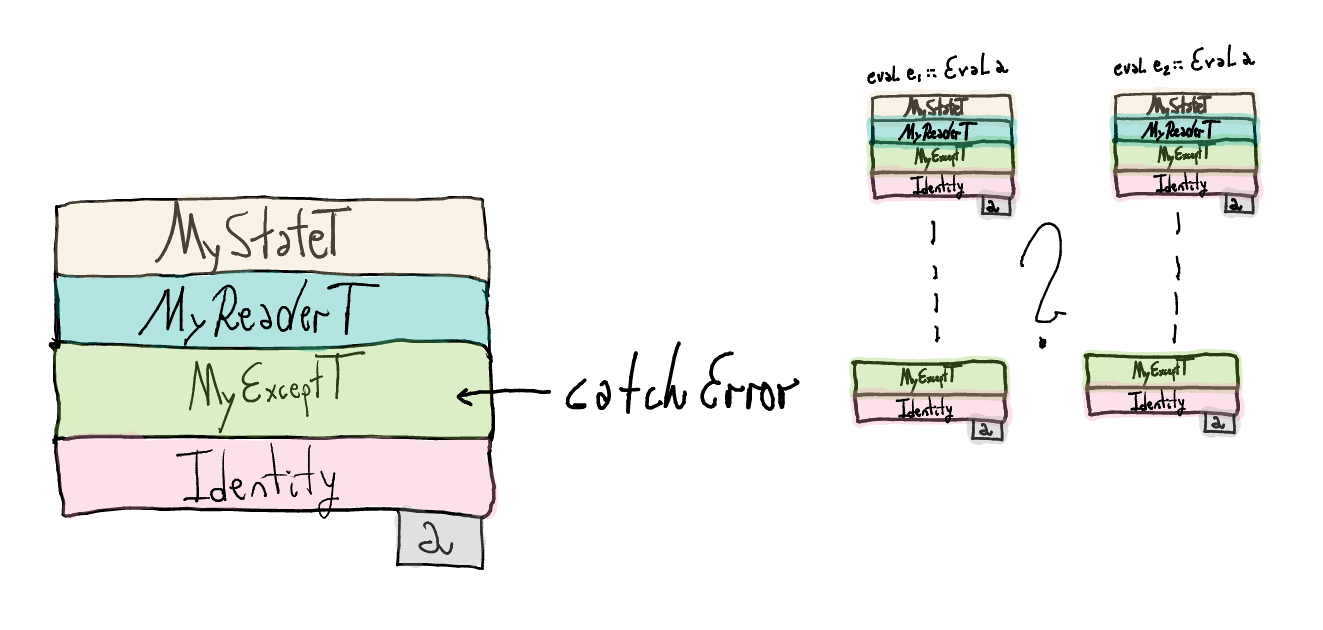
To feed catchError with the appropriate monadic values, we need to run the computations of type Eval a to remove all the upper layers until reaching the right one, i.e., the error layer.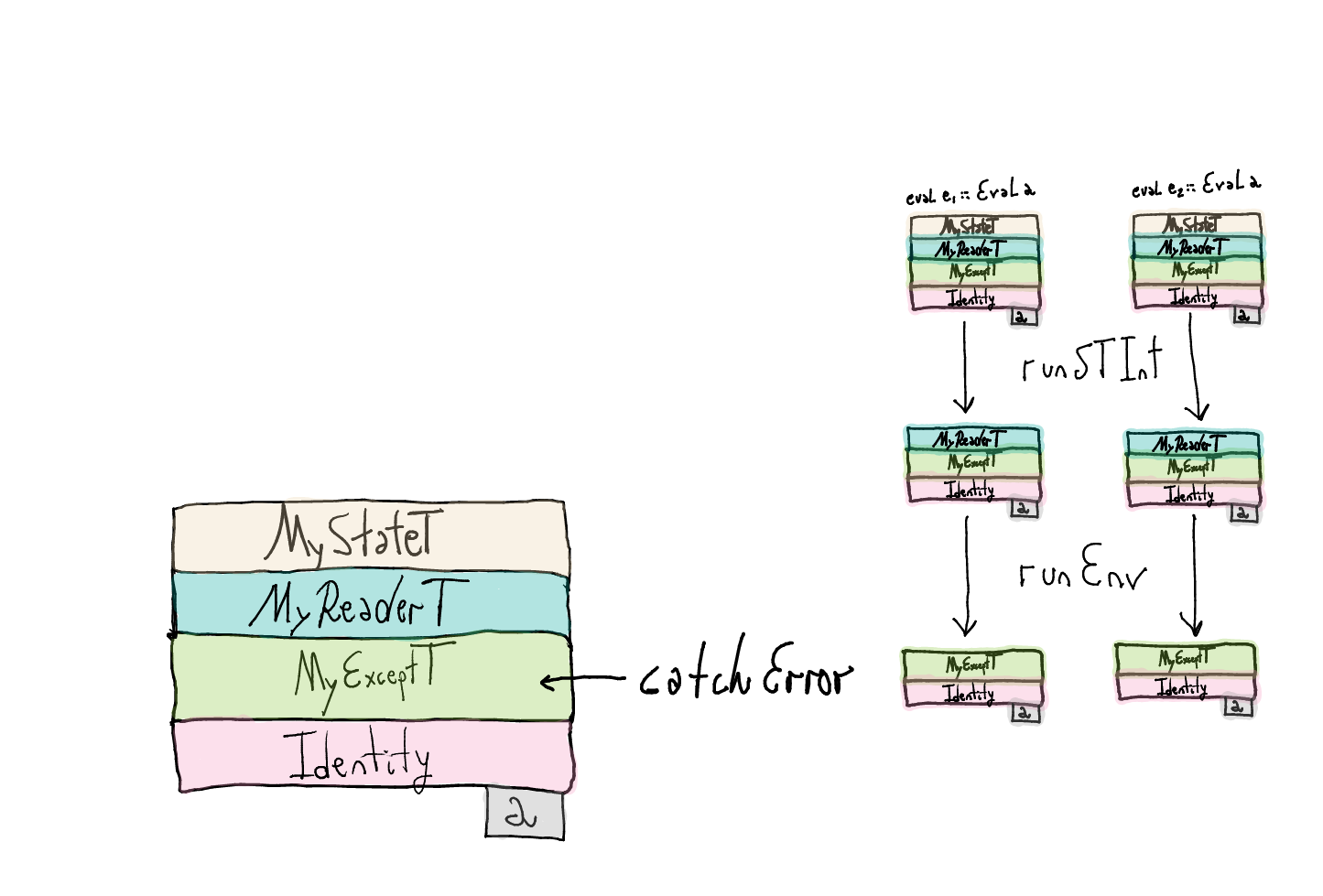

    eval (Catch e1 e2)  =
      let st1  = runSTInt (eval e1)
          st2  = runSTInt (eval e2)
          ...

So far, we obtained functions st1 and st2 which produce, when given an state, a monadic computation in the next layer of the stack (i.e., a reader monadic computation). In other words, to run st1 and st2, and therefore going deeper into the monad stack, it is necessary to provide a state. Since we have none in scope, we need to break the abstraction of the MyStateT monad transformer in order to introduce a binding for the state.

    eval (Catch e1 e2) = MyStateT \ s -> do
      let
        st1  = runSTInt (eval e1)
        st2  = runSTInt (eval e2)
        env1 = runEnv (st1 s)
        env2 = runEnv (st2 s)
      ...

At this point, we are at the level of the reader monad in our stack.

Function env1 and env2 produce, when given an environment, a computation in the error layer monad. As before, since we do not have an environment in scope, we need to break the abstraction of the MyReaderT monad transformer to introduce a binding for the environment.

  eval (Catch e1 e2) = MyStateT \ s -> do
    let
      st1  = runSTInt (eval e1)
      st2  = runSTInt (eval e2)
      env1 = runEnv (st1 s)
      env2 = runEnv (st2 s)
    MyReaderT \ r  -> ...

With the environment r in scope, env1 r :: MyExceptT Err Identity a and env2 r :: MyExceptT Err Identity a and we can feed function catchError with them.

   eval (Catch e1 e2) = MyStateT \ s -> do
     let
       st1  = runSTInt (eval e1)
       st2  = runSTInt (eval e2)
       env1 = runEnv (st1 s)
       env2 = runEnv (st2 s)
     MyReaderT \ r  -> catchError (env1 r) (\ _err -> env2 r)

We have not described how to adapt the function localScope and we leave it as an exercise since it exhibits a similar problem as eval (Catch e1 e2).
In Interpreter 4, GHC's "deriving magic" saves you from all the complications of lifting non-proper morphisms.

If you design your own monad transformer, however, it is highly probably that GHC does not know how to derive it.

Summary

The combination of effects does not always compose.
- The order in which monad transformers are applied matters
- It is not semantically the same to first apply the state and then the error monad transformer, than the other way around
We show implementations for state, error, and reader monad transformers.
Lifting non-proper morphism is not always trivial.
- Sometimes, we need to break the abstraction of upper layers until we get to the layer where the non-proper morphism resides, apply it, and then lift the result back to the top layer by either applying the monad transformers' constructors or the right amount of lift functions.

Monad transformers II: composition of error and state transformers

The except (error) monad transformer

Composition of effects

Interpreter 3: ExceptT on the inside

Interpreter 4: ExceptT on the outside

Which one is better? ExceptT outside or inside?

Interpreter 5: Adding I/O

Implementing monad transformers

MyStateT: a state monad transformer

Monad transformers: lifting non-proper morphisms

MyExceptT: an error monad transformer

MyReaderT: a reader monad transformer

Interpreter 6: an interpreter with MyStateT, MyExceptT, and MyReaderT

Lifting operations I

Lifting operations II

Summary

Interpreter 3: `ExceptT` on the inside

Interpreter 4: `ExceptT` on the outside

`MyStateT`: a state monad transformer

`MyExceptT`: an error monad transformer

`MyReaderT`: a reader monad transformer

Interpreter 6: an interpreter with `MyStateT`, `MyExceptT`, and `MyReaderT`