Monad transformers

Motivation

Programs often perform several side-effects
- Error reporting
- Stateful computations
- I/O
So, you can imagine a super-monad that does all of that
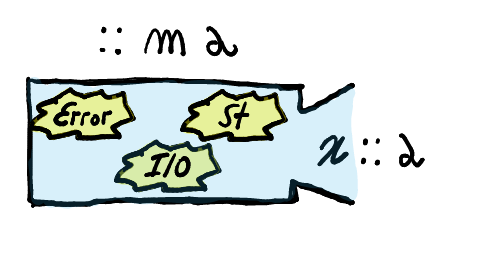
What happens if I need a monad with less effects?
- Redefine that definition for m a, adapt return and (>>=) as well as the non-proper morphisms.
What happens if I need a monad with more effects?
- Redefine that definition for m a, adapt return and (>>=) as well as the non-proper morphisms.
We want to compose effects in a modular manner.

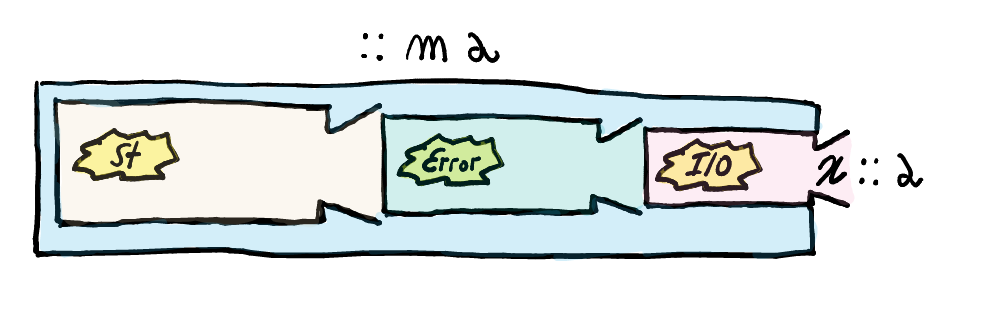
We would like non-proper morphisms, return, and (>>=) require minimum modifications when effects are added/removed.
Monad transformers help us to do that.

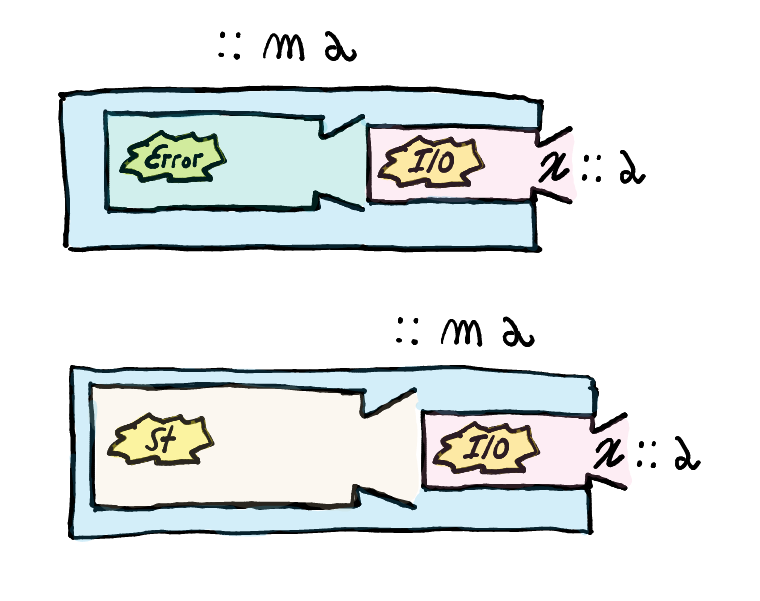It allows us to combine effects on demand!

Not all the possible combinations of effects can be modularly combined!

Monad transformers are not the perfect solution, but they certainly helps (we will discuss more of the consequences of combining effects in the next lecture).

Running example: a simple interpreter

During this lecture, we consider a simple monadic interpreter.
The interpreter underlying monad is going to be modularly enhanced with different effects.

A simple (non-monadic) interpreter of expressions:

data Expr = Lit Integer
          | Expr :+: Expr

s_eval :: Expr -> Integer
s_eval (Lit n)     = n
s_eval (e1 :+: e2) = s_eval e1 + s_eval e2

This code is not monadic, but we can change that.

Interpreter0: no side-effects

code

Any code can be "lifted" into the identity monad, i.e., a monad with no side-effects.
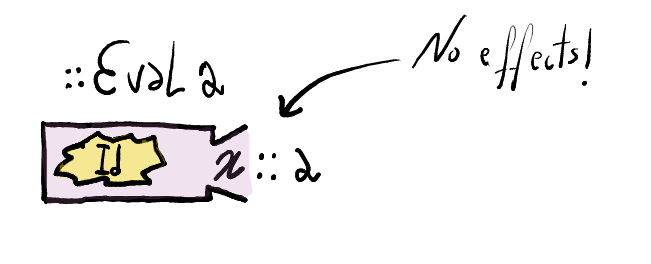
```
import Control.Monad.Identity
type Eval a = Identity a
```
Type Eval a denotes a monadic computation.
We change the type of the interpreter to return a monadic computation
```
eval :: Expr -> Eval Integer
eval (Lit n)   = return n
eval (a :+: b) = (+) <$> eval a <*> eval b
```
We leverage the function runIdentity :: Identity a -> a to run the interpreter.
```
runEval :: Eval a -> a
runEval = runIdentity
```
There are no effects, it just computes the result. More formally, we have that
```
runEval . eval  ≡  s_eval
```
We want to extend our interpreter with new features
- Local declarations
- Exceptions
- References
How are we going to extend the Eval monad?

Enter monad transformers

Monad transformers are type-level functions
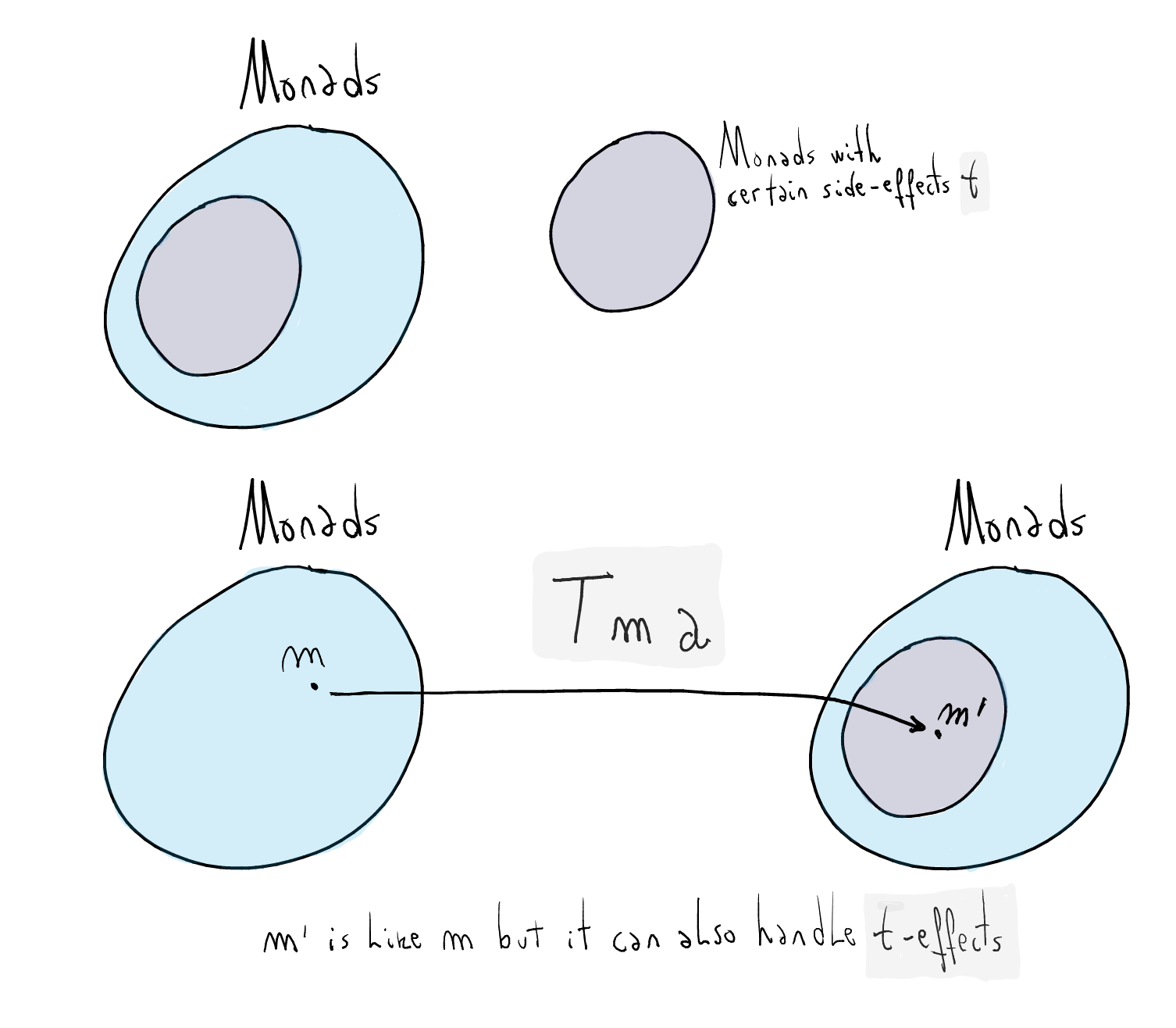
A certain monad transformer T takes a monad m and produces a monad with additional side-effects
Every monad transformer T maps monads into a set of monads with the side-effects added by T

Interpreter1: the reader monad transformer

code

We want to extend our language of expression with local bindings, e.g., we would like to run a program like let x = 5; x+x.

We extend our data type for expressions:

data Expr = Lit Integer
          | Expr :+: Expr
          | Var Name            -- new
          | Let Name Expr Expr  -- new

Bindings are immutable, i.e., once a variable is bound to a value, it cannot be changed.
Expression can now involve bound variables, e.g., x+y.
To evaluate expressions, eval should include an immutable environment which contains the values for bound variables.
We model environments as mappings from variables names to values, i.e., think it a mapping as an element of type [(Name, Value)] or Name -> Maybe Value.

We use mappings from the module Data.Map:
```
type Env = Map Name Value

emptyEnv = Map.empty
Map.lookup :: Ord k => k -> Map k a -> Maybe a
Map.insert :: Ord k => k -> a -> Map k a -> Map k a
```
We would like to implement a monad with a read-only environment since bindings are immutable.
One alternative is to hard-wire it into the interpreter:
```
eval :: Env -> Expr -> Eval Value
```
This means that there would be some plumbing to pass the environment between recursive calls (recall lecture 3).
Instead, we use the monad transformer ReaderT to add a read-only state into the Eval monad!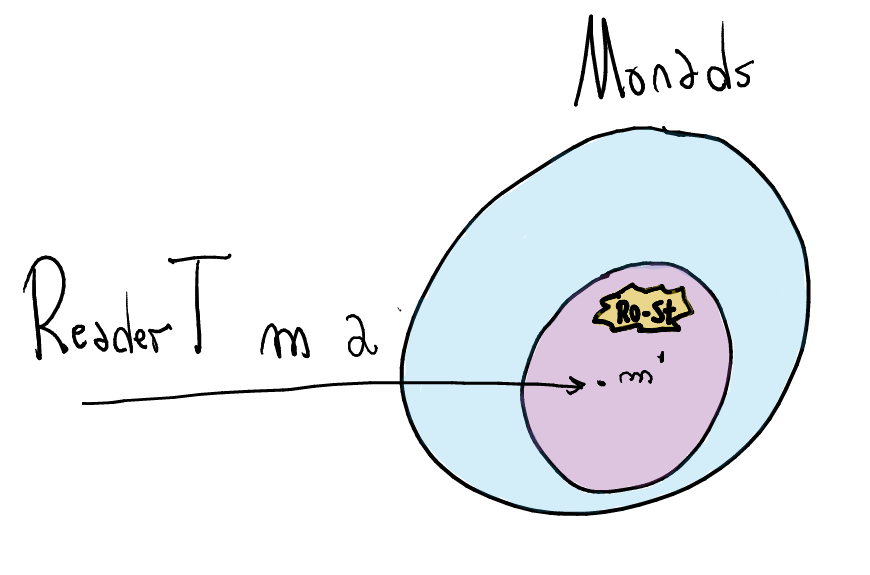

In other words, ReaderT takes a monad m and returns a monad which support two operations: local and ask — such monads are called MonadReader.

A monad obtained by the transformer `ReaderT` is a `MonadReader`, but not all `MonadReader`s are obtained by using the monad transformer `ReaderT`!
```
type ReaderT r m a

runReaderT :: ReaderT r m a -> (r -> m a)

class Monad m => MonadReader r m where
  ask   :: m r
  local :: (r -> r) -> m a -> m a

instance Monad m => Monad         (ReaderT r m)
instance Monad m => MonadReader r (ReaderT r m)
```
Implementation:
```
newtype ReaderT r m a = ReaderT { runReaderT :: r -> m a }
```
The monad Eval is then responsible for the plumbing required to pass around the environment.
```
{-# LANGUAGE GeneralisedNewtypeDeriving #-}

newtype Eval a = Eval { unEval :: ReaderT Env (Identity) a }
  deriving (Functor, Applicative, Monad, MonadReader Env)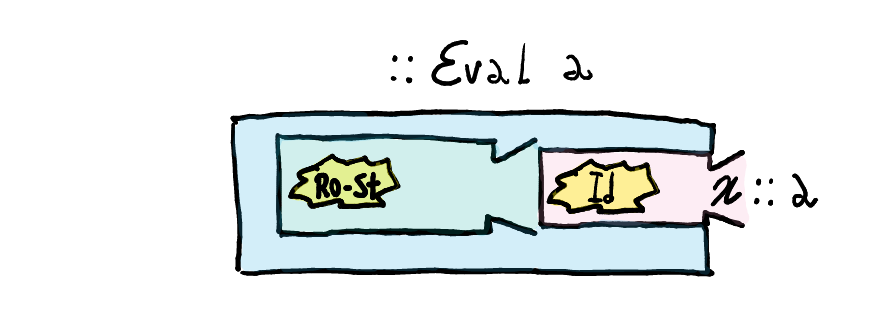
```
We introduce a new data type, rather than just a type synonym, because we want Haskell to derive some type-classes instances.

Due to instance MonadReader Env Eval, our evaluation monad supports
```
ask   :: Eval Env
local :: (Env -> Env) -> Eval a -> Eval a
```
Let us define some environment manipulation based on local and ask.

Looking up the value of a variable in the enviroment.
```
lookupVar :: Name -> Eval Value
lookupVar x = do
  env <- ask
  case Map.lookup x env of
    Nothing -> error $ unwords ["Variable", x, "not found."]
    Just v  -> return v
```
We can extend the environment with a new binding for a local computation. Since we are using a reader monad, we can be sure that this binding does not escape outside its intended scope.
```
localScope :: Name -> Value -> Eval a -> Eval a
localScope x v m = local (Map.insert x v) m
```

The interpreter is extended by simply adding cases for the two new constructs. (None of the old cases has to be changed.)

eval :: Expr -> Eval Value
...
eval (Var n)       = lookupVar n                 -- here, we use ask
eval (Let n e1 e2) = do
  v <- eval e1
  localScope n v (eval e2)                       -- here, we use local

The run function simply runs the interpreter with the initial empty environment.
```
runEval :: Eval a -> a
runEval m = runIdentity (runReaderT (unEval m) emptyEnv)
```
Observe how we run the reader monad first, and then the identity monad.

When using monad transformers, you start running the outermost monad and finish with the innermost one of your monad stack.

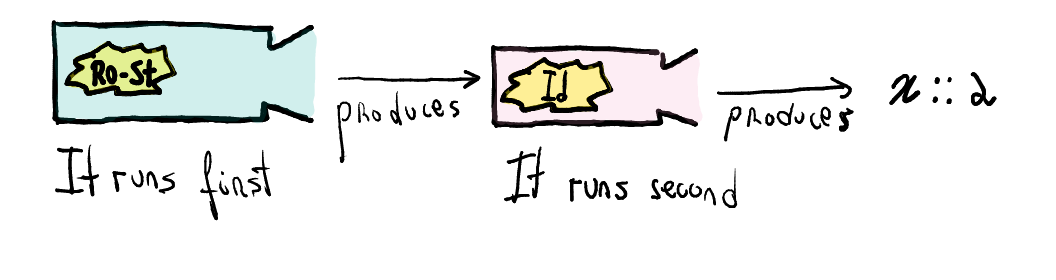
The textual ordering of runners in runEval is reversed w.r.t. the ordering of type constructors in newtype Eval. We can get the same textual order with reverse application (&) : a -> (a -> b) -> b and infix sections:
```
newtype Eval a =  Eval   ( ReaderT      Env        Identity    a)
runEval m = m & unEval & (`runReaderT` emptyEnv) & runIdentity
```

Example

runEval $ eval (parse "let x=1+2; x+x")
> 6

Implementation of ReaderT:

newtype ReaderT r m a = ReaderT { runReaderT :: r -> m a }

instance Monad m => MonadReader r (ReaderT r m) where
  ask :: ReaderT r m r
  ask = ReaderT \ r -> return r

  local :: (r -> r) -> ReaderT m a -> ReaderT m a
  local f m = ReaderT \ r -> runReaderT m (f r)

instance Monad m => Monad (ReaderT r m) where
  return :: a -> ReaderT r m a
  return a = ReaderT \ r -> return a

  (>>=) :: ReaderT r m a -> (a -> ReaderT r m b) -> ReaderT r m b
  m >>= k = ReaderT \ r -> do
    a <- runReaderT m r
    b <- runReaderT (k a) r
    return b

Exercise:

Do we have Applicative m => Applicative (ReaderT r m)?
Can you implement the interpreter with just the Applicative interface (no Monad)?

Interpreter 2: the state monad transformer

code

We want to extend our language of expression with mutable references, e.g., we would like to run a program like let r = new 7; !r+!r
We add new constructors in our expressions language for creation, reading, and writing of references.
```
data Expr = Lit Integer
          | Expr :+: Expr
          | Var Name
          | Let Name Expr Expr
          | NewRef Expr         -- new
          | Deref Expr          -- new
          | Expr := Expr        -- new
```
Expression NewRef e creates a fresh reference which initially contains the value denoted by e.

Expression Deref e denotes the value stored by the reference denoted by e.

Expression e1 := e2 changes the value stored in the reference denoted by e1 with the value denoted by e2.
The interpreter needs a notion of memory or store to keep the values stored in references.
This store is mutable, since references are mutable too!
We represent it as a mapping from memory locations to values:
```
type Ptr   = Integer
data Store = Store
  { nextPtr :: Ptr
  , heap    :: Map Ptr Value
  }
```
A Store is then a mapping from a value denoting a memory location to the value stored at that location.

For instance, the following mapping
```
Map.insert 2 42 (Map.insert 1 7 (Map.insert 0 101 Map.empty))
```
denotes a memory with three references: at location 0 with value 101, at location 1 with value 7, and at location 2 with value 42.

We also remember the next unused pointer as part of the store (useful when allocating a new reference).
```
emptyStore :: Store
emptyStore = Store 0 Map.empty
```
As before, one alternative is to hard-wire it into the interpreter
```
eval :: Store -> Expr -> Eval Value
```
This means that there would be some plumbing to pass the store (memory) between recursive calls (recall lecture 3).
Instead, we use the monad transformer StateT to add a mutable state into the Eval monad!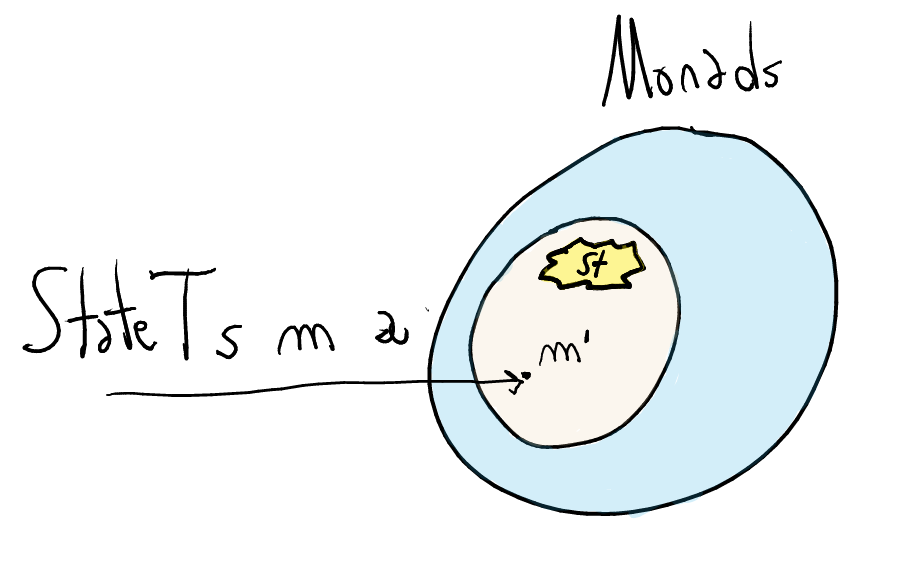

In other words, StateT takes a monad m and returns a monad which contains a mutable state of certain type s and two operations: get and put — such monads are called MonadState s. (Actually, they have one more operation (state) but we will not describe it here)
```
data StateT s m a

evalStateT :: Monad m => StateT s m a -> s -> m a

class Monad m => MonadState s m where
  get :: m s
  put :: s -> m ()
```

The monad Eval is then responsible for the plumbing required to pass around the store.

newtype Eval a = Eval { unEval :: StateT Store (ReaderT Env Identity) a }
  deriving (Functor, Applicative,
            Monad, MonadState Store, MonadReader Env)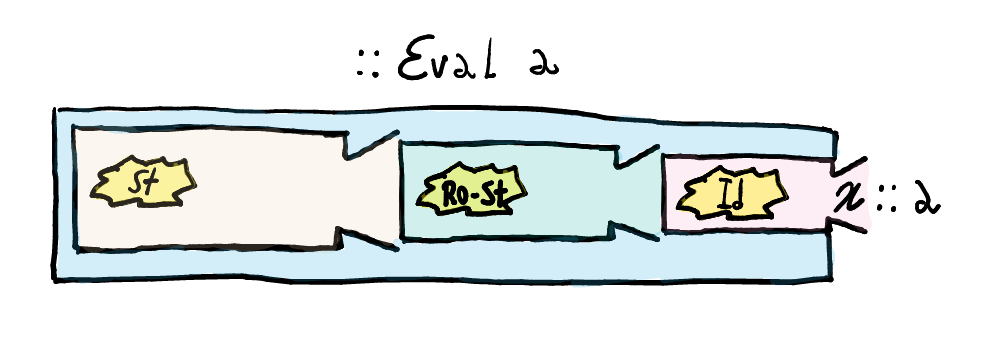

Alternatively, we could have defined an state-reader monad from scratch, i.e., not using the monad transformers

newtype Eval a = Eval { unEval :: Store -> Env -> (a, Store) }

**Exercise**: Implement a "state-reader monad" directly

newtype MyMonad s e a = MyMonad {runMyMonad :: s -> e -> (a,s)}

instance Monad (MyMonad s e) where
  return = returnMyMonad
  (>>=)  = bindMyMonad
returnMyMonad :: a -> MyMonad s e a
returnMyMonad x = MyMonad \ s  -> \ e -> (x, s)

While it works, the price to pay is modularity.

Let us define some operations for the interpreter based on get and put:

Creation of a new reference: modify both the next available memory location and the heap.

newRef :: Value -> Eval Ptr
newRef v = do
  store <- get
  let ptr      = nextPtr store
      new_ptr  = 1 + ptr
      newHeap  = Map.insert ptr v (heap store)
  put Store{ nextPtr = new_ptr, heap = newHeap }
  return ptr

Getting the value of a reference: look up a memory location in the store. We crash with our own "segfault" if given a non-existing pointer (observe that the state has not been changed.)

deref :: Ptr -> Eval Value
deref p = do
  st <- get
  let h = heap st
  case Map.lookup p h of
    Nothing -> error $ unwords ["'Segmentation fault':", show p, "is not bound."]
    Just v  -> return v

Updating a reference: change a value in the store.

(=:) :: MonadState Store m => Ptr -> Value -> m Value
p =: v = do
  store <- get
  let updt_heap = Map.adjust (const v) p (heap store)
  put store{ heap = updt_heap }
  return v
-- Map.adjust :: (Ord k) => (a -> a) -> k -> Map k a -> Map k a

Observe that (=:) has no effect if the reference does not exist.

**Exercise**: Maybe that is not the best semantics. What would it be a better one?

We define the evaluation of expressions for the new cases with the functions described above.

eval :: Expr -> Eval Value
...
eval (NewRef e) = do
  v <- eval e
  newRef v
eval (Deref e)  = do
  p <- eval e
  deref p
eval (pe := ve) = do
  p <- eval pe
  v <- eval ve
  p =: v

As before, we do not need to change the definition for the old constructors.

We can test it:

> runEval $ eval $ parse "let p=new 7; !p"
7

Unfortunately, our expression language supports pointer arithmetic (like C), so a pointer might dereference another one — a recipe for disaster!
```
> runEval $ eval $ parse "let p=new 1; let q=new 1738; !(p+1)"
1738
```
How are we going to fix it?

(Discuss solutions.)
What else can go wrong with our interpreter?

Expressions might refer to unbound variables / references.
```
> runEval $ eval $ parse "q + 1"
*** Exception: Variable q not found.
```
```
> runEval $ eval $ parse "!q"
*** Exception: Variable q not found.
```
We need some exception handling mechanism into the language of expressions.

Summary

Programs often handle more than one effect
Monad transformer are type-level functions which allow one to extend existing monads with additional side-effects
- The deriving mechanisms in Haskell is quite powerful and promote re-utilization of code
- Monad transformers are not essential and you can create your own monad with all the effects that you need. The problem? Modularity, i.e., code rewritten if you need to change your monad to add a new effect.