Functors, Applicative, and Monads

A simple monadic EDSL for input/output (deep embedding)

We will develop a simple I/O EDSL in Haskell

-- Types
type Program a

-- Constructors
return :: a -> Program a
putC   :: Char -> Program ()
getC   :: Program (Maybe Char)

-- Combinators
(>>=) :: Program a -> (a -> Program b) -> Program b

-- Run function
type IOSem a
run :: Program a -> IOSem a

We use monads to sequence I/O effects.
Scenario

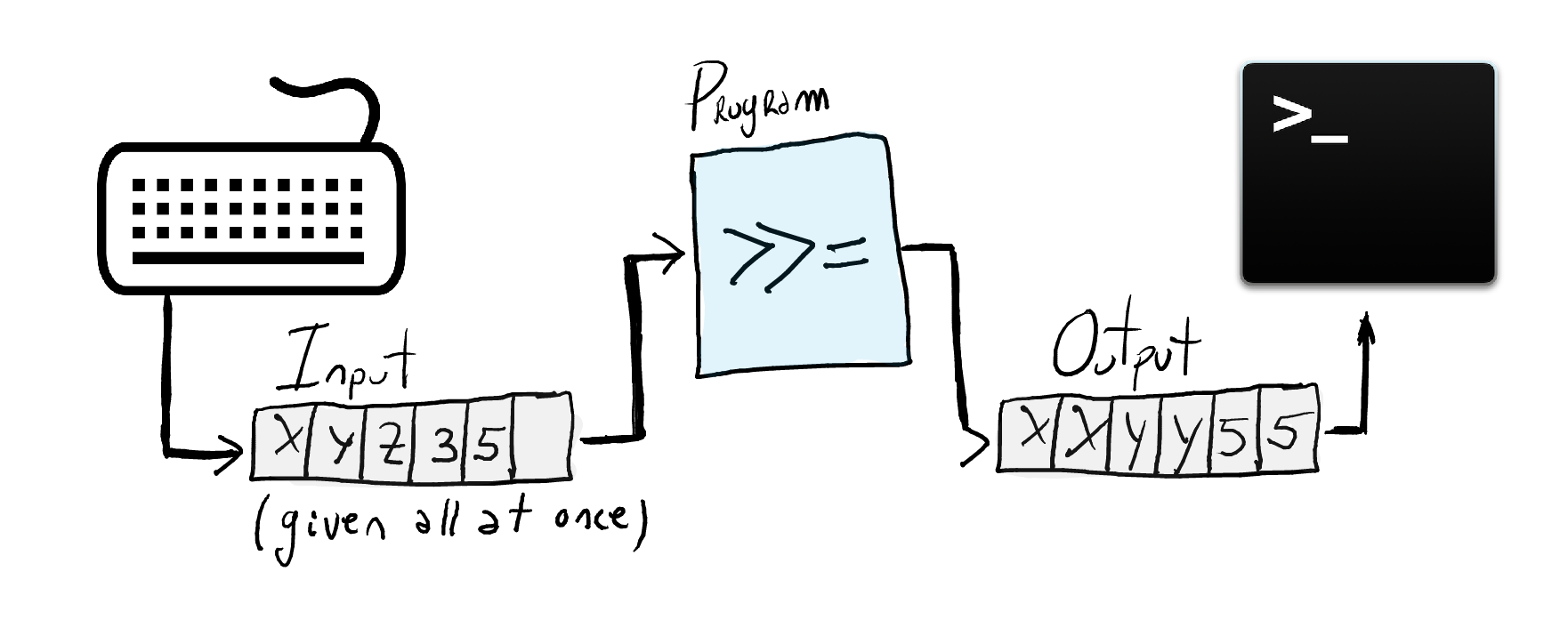
Types for inputs and outputs

type Input   =  String
type Output  =  String

Following the deep embedding guidelines, we have a constructor in Program per constructor / combinator.
```
data Program a where
  Put    :: Char -> Program ()
  Get    :: Program (Maybe Char)
  Return :: a -> Program a
  Bind   :: Program a -> (a -> Program b) -> Program b
```
Observe the use of GADTs!
- In the definition of Get, why using Maybe Char instead of Char?
- We need to indicate the "end of input" somehow, i.e., by using Nothing
```
getC = Get
putC = Put
```
What's the implementation of the type IOSem, i.e., the semantics of a program?
```
type IOSem a = Input -> (a, Input, Output)
```
It is a function which takes an input and returns a result (of type a), the left over input (of type Input), and an output (of type Output).

The run function

 run :: Program a -> IOSem a
 run (Put c)    inp     =  (()     , inp  , [c]           )
 run (Get)      ""      =  (Nothing, ""   , ""            )
 run (Get)      (c:cs)  =  (Just c , cs   , ""            )
 run (Return x) inp     =  (x      , inp  , ""            )
 run (Bind m k) inp     =  (b      , inp_b, out_a ++ out_b)
   where
     (a, inp_a, out_a) = run m inp
     (b, inp_b, out_b) = run (k a) inp_a

Let us write an "echo" program
```
echo :: Program ()
echo = getC >>= \case
  Nothing -> return ()
  Just c  -> putC c
```
To run it, we need to give it an input
```
run echo "a"
> ((), "", "a")
```
Exercise: write a program which does a double echo, i.e., it reads a character from the input and writes it twice into the output.

A simple monadic EDSL for input/output (intermediate embedding)

code

It is often good to move away a bit from the pure deep embedding towards some kind of "normal form" ("optimized", "elemental" embedding).
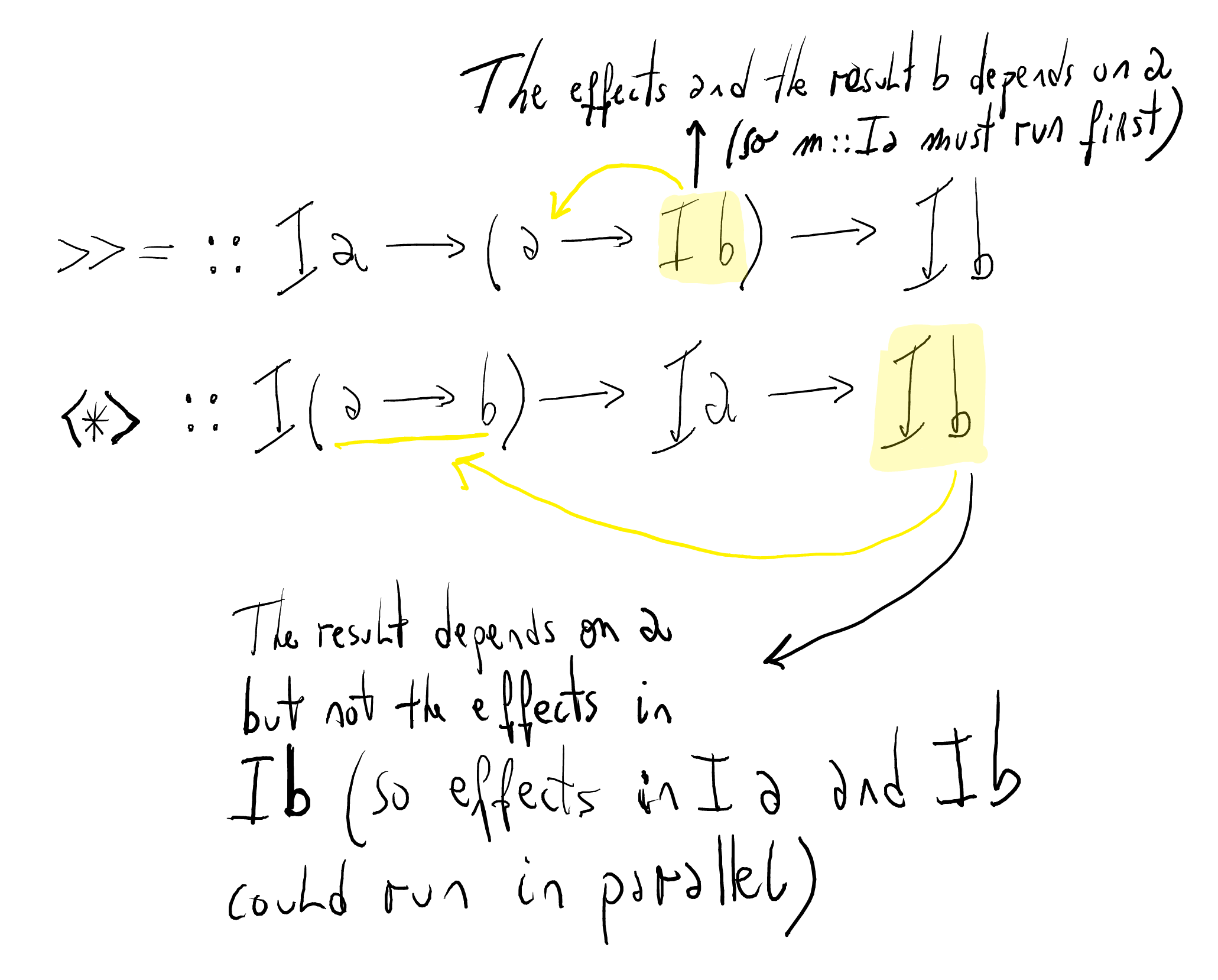
We want to remove the Bind operator. (This, done correctly, will turn Program into a lawful monad.) How are we going to write sequential actions then?

`(>>=)` is going to be executed when constructing the program, but not when running it!
Methodology:
- Looking the most typical usage patterns of Bind,
- Introduce new constructors to capture such cases, and
- Simplify the data type with the new constructors
Let's look at the different cases for the first argument of Bind.
```
  Put c    >>= f
  Get      >>= f
  Return x >>= f
```
```
Put c >>= f
```
From the types of Put and Bind we note that f must have type
```
() -> m a
```
which is basically just a value of type m a. Another way to think about it is that Put does not really return any useful value (the actual "putting" is implemented as a "side-effect"). So the function after bind can ignore its argument.
```
Put c >>= \ _ -> p  ≡  Put c >> p
```
We will now give a name to this new combination
```
PutThen c p  ≡  Put c >> p
```
This is a Program which starts by printing c and the behaves like p.
```
Get >>= f
```
In a similar way we can introduce a new name for the combination of Get and Bind:
```
GetBind f  ≡  Get >>= f
```
```
Return x >>= f
```
The third combination would be ReturnBind
```
ReturnBind x f  ≡  Return x >>= f
```
but the first monad law already tells us that this is just (f x) so no new constructor is needed for this combination.
For the last combination, i.e., (m >>= g) >>= f, the associative monadic law tells us how we can rewrite it.

We then define Program using the first two combinations and return:

data Program a where
  PutThen :: Char -> Program a         -> Program a
  GetBind :: (Maybe Char -> Program a) -> Program a
  Return  :: a                         -> Program a

Observe that the data type is a regular Haskell data type and it does not use any of the features of a GADT.

One way to think about PutThen and GetBind is with continuations. For instance, PutThen c p writes a character into the output of the program and continues behaving as p. Similarly, Get f reads maybe a character mc from the input and continues behaving as program f mc.
```
putC :: Char -> Program ()
putC c = PutThen c $ Return ()
```
Function putC writes a character in the output and then it behaves as Return ()
```
getC :: Program (Maybe Char)
getC = GetBind Return
```
Function getC reads maybe a character from the input and, once that is done, it behaves as Return ()
The bind is not going to be a part of the Program data structure, but rather part of the instance Monad, i.e., the bind is not deeply implemented as a constructor (intermediate embedding)

Calculating `(>>=)` for `Program` as a monad (intermediate embedding)

What is the definition for bind?

instance Monad Program where
    return :: a -> Program a
    return = Return

    (>>=) :: Program a -> (a -> Program b) -> Program b
    PutThen c p >>= k   =  ?
    GetBind f   >>= k   =  ?
    Return x    >>= k   =  ?

We can calculate the correct definition of `(>>=)` using the definitions of `PutThen`, `GetBind`, and the monadic laws!

Case Return x:
```
Return x >>= k = k x
```
This is dictated by the first monad law!

Case GetBind f:

GetBind f >>= k = ?

GetBind f >>= k
  = { Def. GetBind }
(Get >>= f) >>=  k
  = { Law 3.  (m >>= f) >>= g  ≡  m >>= (\ x -> f x >>= g)
      with m = Get, f = f, g = k }
Get >>= (\ x -> f x >>= k)
  = { Def. GetBind }
GetBind (\ x -> f x >>= k)

GetBind f >>= k = GetBind (\ x -> f x >>= k)

Case PutThen c p:

PutThen c p >>= k = ?

PutThen c p >>= k
  = { Def. of PutThen }
(Put c >> p) >>= k
  = { Def. of (>>) }
(Put c >>= \ _ -> p) >>= k
  = { Law3 with m = Put c, f = (\ _ -> p), g = k }
Put c >>= (\ x -> (\ _ -> p) x >>= k)
  = { simplify }
Put c >>= (\ _ -> p >>= k)
  = { Def. of (>>) }
Put c >> (p >>= k)
  = { Def. of PutThen }
PutThen c (p >>= k)

PutThen c p >>= k =  PutThen c (p >>= k)

So, we can now complete defining Program as a monad

instance Monad Program where
    return  = Return

    PutThen c p >>= k   =  PutThen c (p >>= k)
    GetBind f   >>= k   =  GetBind (\ x -> f x >>= k)
    Return x    >>= k   =  k x

A simple monadic EDSL for input/output (shallow embedding)

This is an exercise for you to do!

Please, check the code skeleton for that.

Monads

A structure that represents computations defined as sequences of steps.

The bind operator `(>>=)` defines what it means to chain operations of a monadic type.
In this lecture, we will learn about two other structures useful in functional programming
- Functors
- Applicative functors

Structure-preserving mappings

We are familiar with the map function over lists
```
map (+ 1) [2,3,4,5,6]
```
which applies the function (+ 1) to every element of the list, and produces the list
```
[3,4,5,6,7]
```

We can generalize the concept of map to work on trees

data Tree a = Leaf a | Node (Tree a) (Tree a)

mapTree :: (a -> b) -> Tree a -> Tree b
mapTree f (Leaf a)     = Leaf (f a)
mapTree f (Node t1 t2) = Node (mapTree f t1)
                              (mapTree f t2)

As we did with lists, we can apply the function (+ 1) at every element of the data structure.

For instance,

mapTree (+ 1) $
  Node (Leaf 2) (Node (Node (Leaf 3) (Leaf 4)) (Leaf 5))

produces the following tree.

  Node (Leaf 3) (Node (Node (Leaf 4) (Leaf 5)) (Leaf 6))

In both cases, the structure of the data type (i.e., lists and trees) is preserved
General pattern:

It is useful to apply functions to data types elements while respecting the structure (shape) of it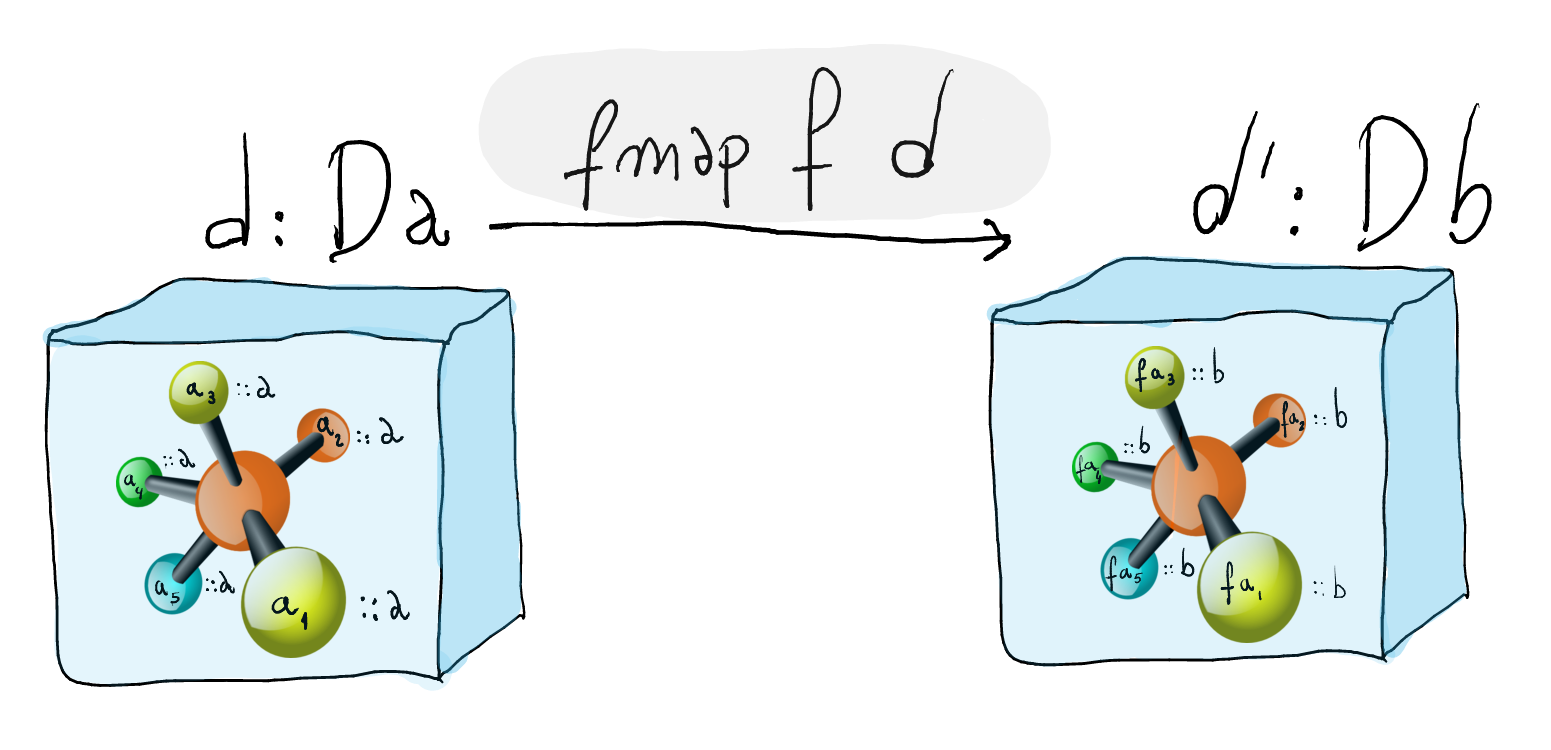

Functors

A functor is composed of two elements: a parametrized data type definition (container) and a generalized map-function called fmap.
In Haskell, fmap is an overloaded function, i.e., defined for every container which supports a map-like operation.
```
class Functor d where
    fmap :: (a -> b) -> d a -> d b
```
A functor must obey the following laws.
Name Law
Identity:
fmap id ≡ id
Map fusion (or composition):
fmap (f . g) ≡ fmap f . fmap g
Observe that *map fusion* allows to reduce two traversals to one!

Name	Law
Identity:	fmap id ≡ id
Map fusion (or composition):	fmap (f . g) ≡ fmap f . fmap g

Let us consider again the Tree example

instance Functor Tree where
  fmap f (Leaf a)     = Leaf (f a)
  fmap f (Node t1 t2) = Node (fmap f t1) (fmap f t2)

Now, we can write

(+ 1) `fmap` (Node (Leaf 2) ((Node (Node (Leaf 3) (Leaf 4)) (Leaf 5))))

Functors: more examples

Maybe data type
```
(+ 1) `fmap` (Just 10)
```

Generalized trees

data TreeG a = LeafG a | BranchG [TreeG a]

instance Functor TreeG where
  fmap f (LeafG a)    = LeafG (f a)

What about BranchG? We will use the fmap from lists!

fmap f (BranchG ts) = BranchG (fmap (fmap f) ts)

The outermost fmap is the one corresponding to lists.

For instance, the expression

(+ 1)
`fmap` BranchG [LeafG 10,
                BranchG [LeafG 11, LeafG 12],
                BranchG [LeafG 13, LeafG 14, LeafG 15]]

produces

BranchG [LeafG 11,
        BranchG [LeafG 12, LeafG 13],
        BranchG [LeafG 14, LeafG 15, LeafG 16]]

To summarize:

Functors simplifies boilerplate code, i.e., destructing a container in order to create another one!

As data types can be built from other ones, so do functors! (thus achieving modularity)

Multi-parameter functions map to multiple containers

In a more general case, sometimes we would like to transform elements in a container (data type) based on applying a "multi-parameter function" to multiple containers (the quotes are there since in Haskell every function has exactly one argument due to curryfication)
Keep in mind that fmap takes a function of type a -> b and not "multi-parameter" ones, e.g., a -> b -> c
Let us take as an example to see what happens when fmap is used with a "multi-parameter" function.
```
fmap2 :: (a -> b -> c) -> Maybe a -> Maybe b -> Maybe c
fmap2 f ma mb =
  let m_b_to_c = fmap f ma
  in  undefined
```
Once we apply fmap to the first container, we have a container (m_b_to_c) with a function of type b -> c in it.

To keep applying f, what we need to do is to take its partial application out of the container m_b_to_c and mapped over mb, where its next argument is located.
```
fmap2 :: (a -> b -> c) -> Maybe a -> Maybe b -> Maybe c
fmap2 f ma mb =
  let m_b_to_c = fmap f ma
  in  case m_b_to_c of
        Nothing -> Nothing
        Just fa -> fmap fa mb
```
What about zero parameters?
```
fmap0 :: a -> Maybe a
fmap0 = Just
```
What happens if function f has even more arguments? E.g. arity three:
```
 fmap3 :: (a -> b -> c -> d) -> Maybe a -> Maybe b -> Maybe c -> Maybe d
 fmap3 f ma mb mc =
   case fmap f ma of
     Nothing -> Nothing
     Just fa -> case fmap fa mb of
        Nothing  -> Nothing
        Just fab -> fmap fab mc
 
```
To solve this for all arities, we need code to extract partial application of functions out from containers, applied them, and wrap the result in another container!

Applicative functors (see below) are conceived to do precisely this work!

Laws for multi-parameter maps.

Beside identity law for fmap, namely fmap id ≡ id, we need an infinite family of composition laws:
- fmap f (fmap g m1) ≡ fmap (\ x1 -> f (g x1)) m1
- fmap f (fmap2 g m1 m2) ≡ fmap2 (\ x1 x2 -> f (g x1 x2)) m1 m2
- fmap2 f m1 (fmap g m2) ≡ fmap2 (\ x1 x2 -> f x1 (g x2)) m1 m2
- fmap2 f (fmap g m1) m2 ≡ fmap2 (\ x1 x2 -> f (g x1) x2) m1 m2
- fmap2 f (fmap3 g m1 m2) m3 ≡ fmap3 (\ x1 x2 x3 -> f (g x1 x2) x3) m1 m2 m3
- ...
- fmap f (fmap0 y) ≡ fmap0 (f y)
- fmap2 f (fmap0 y) m ≡ fmap1 (f y) m
- ...
In the formulation as applicative functors we will need only finitely many laws.

Applicative functors

An applicative functor (or functor with application) is a functor with the following operations.

 class Functor d => Applicative d where
     pure  :: a -> d a
     (<*>) :: d (a -> b) -> d a -> d b

Observe that an applicative functor is a functor.
The pure operation creates a container with the given argument. The interesting operation is idiomatic application (<*>), which we can describe it graphically as follows: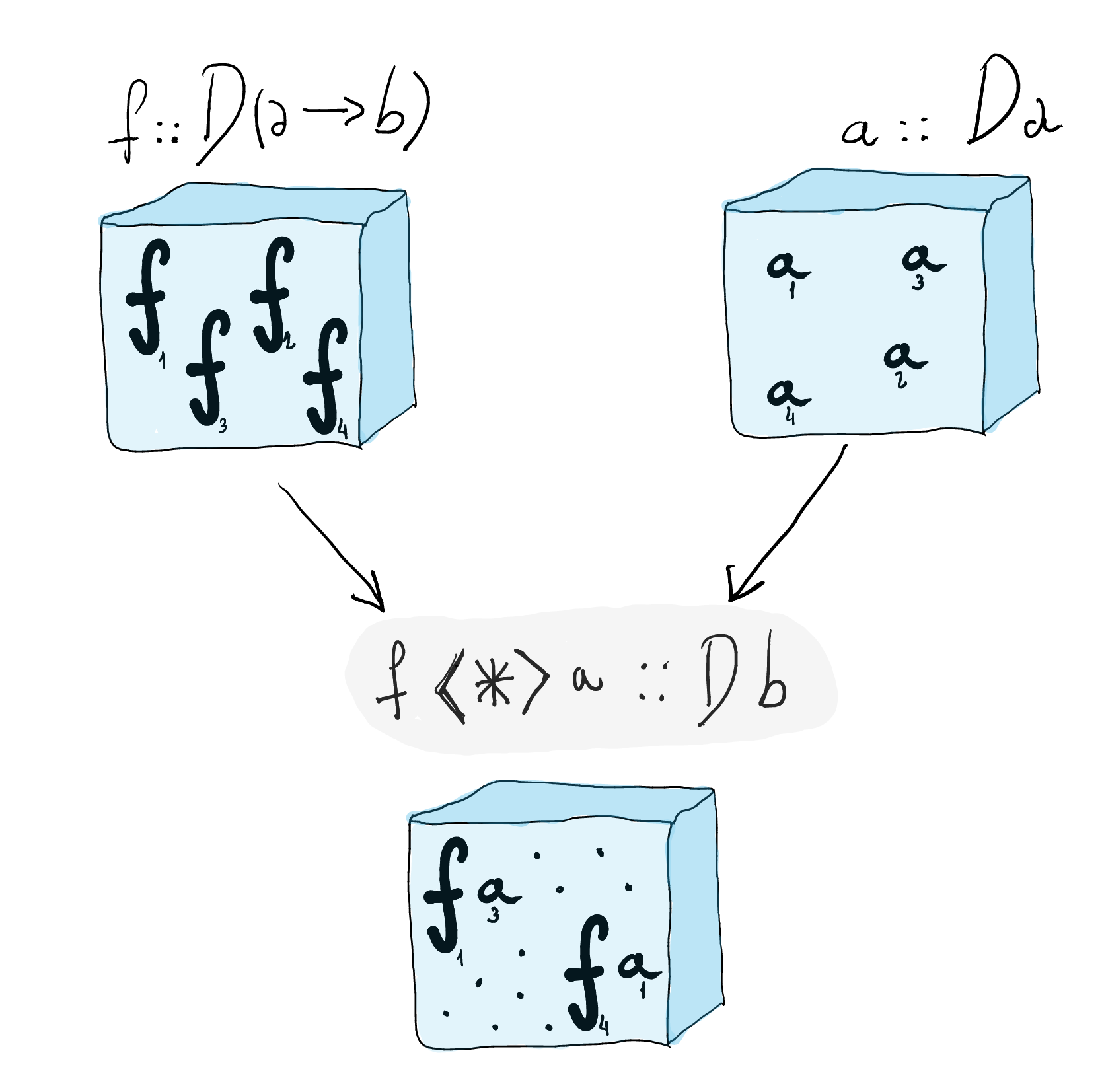

It takes a container of functions and a container of arguments and returns a container of the result of applying such functions.

An applicative functor must obey the following laws:

Name	Law
Identity:	pure id <*> vv ≡ vv
Composition:	pure (.) <> ff <> gg <> zz ≡ ff <> (gg <*> zz)
Homomorphism:	pure f <*> pure v ≡ pure (f v)
Interchange:	ff <> pure v ≡ pure ($ v) <> ff

In the rules above, double letters indicate that the denoted element is in a container, e.g., ff means that it is a function f inside a container, vv is a value which is inside a container and so on.

One of the most interesting rules is interchange. Before explaining it, let us see the types of the expressions involved.

ff :: d (a -> b)
vv :: d a
pure ($ v) :: d ((a -> b) -> b)

The rule says that instead of obtaining a d b as ff <*> pure v, where ff is a container with a function and pure v is its argument, it is possible to apply function ($ v) to the container ff.

Relation to multi-parameter maps: The Haskell names for fmapn are:

fmap0 = pure   ::                    a  ->                         d a
fmap1 = liftA  :: (a1 ->             a) -> d a1 ->                 d a
fmap2 = liftA2 :: (a1 -> a2 ->       a) -> d a1 -> d a2 ->         d a
fmap3 = liftA3 :: (a1 -> a2 -> a3 -> a) -> d a1 -> d a2 -> d a3 -> d a
...

Exercise: Define `liftA`, `liftA2` and `liftA3` for an `Applicative d` and prove (some of) the composition laws.

Applicative Maybe

Let us go back to our example using Maybe

instance Functor Maybe where
    fmap f Nothing  = Nothing
    fmap f (Just a) = Just (f a)

instance Applicative Maybe where
    pure           = Just
    Nothing <*> vv = Nothing
    Just f  <*> vv = fmap f vv

What can we do now with that?
```
-- xx :: Maybe String
-- yy :: Maybe String
pure (++) <*> xx <*> yy
```
We can apply concatenation on strings stored in containers. All the wrapping and unwrapping is handled by the applicative functor.
A common usage pattern of applicative functors is as follows:
```
pure f <*> xx <*> yy <*> zz ...
```
More precisely, a function f in a container as the leftmost term followed by its container arguments!

We can simplify this to
```
f <$> xx <*> yy <*> zz ...
```
using the Functor superclass:
```
(<$>) :: Functor d => (a -> b) -> d a -> d b
(<$>) = fmap
```

Relation to monads

Blog on Applicative Functors

Observe what we have written using the applicative functor Maybe
```
pure (++) <*> xx <*> yy
```
which is equivalent to:
```
liftA2 (++) xx yy
```
If we consider Maybe as a monad instead (which we defined in the previous lecture), we can achieve the same things.
```
do x <- xx
   y <- yy
   return (x ++ y)
```
Since GHC 8.0, there is {-# LANGUAGE ApplicativeDo #-} to desugar the do notation to operations of applicative functors:
```
liftA2 (\ x y -> x ++ y) xx ys
```
In general:
```
do x1 <- e1
   ...
   xn <- en
   return e
```
can be desugared into liftAn (\ x1 ... xn -> e) e1 ... en provided none of the xi appears in any ej.

Can the `ApplicativeDo` desugaring change the meaning of your program? Or is it safe to turn `ApplicativeDo` on by default?

What is the difference between Maybe as an applicative functor or a monad?
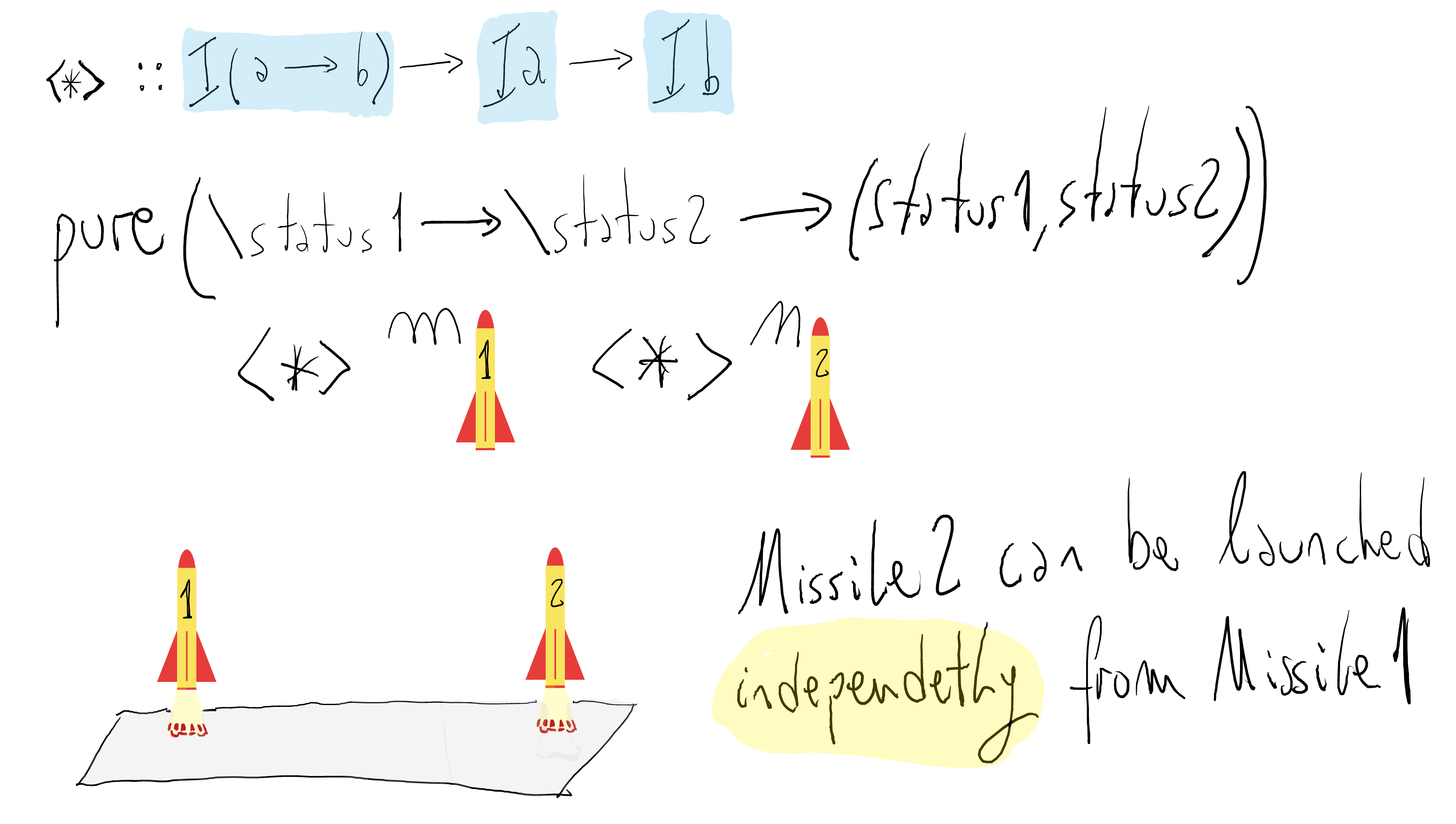
In the case above, both programs produce the same result (x++y). Observe that x gets bound but it is not used until the return instruction — the same occurs with y. However, the effects in a monadic program or an applicative one could be run in a different order.

The difference between monad and applicative functors is the difference between *sequential* vs. *parallel* execution of side-effects.
To appreciate this difference, let us consider a dramatic side-effect: launching a missile. We need to write a program which launches two missiles to a given target.

Monadic code

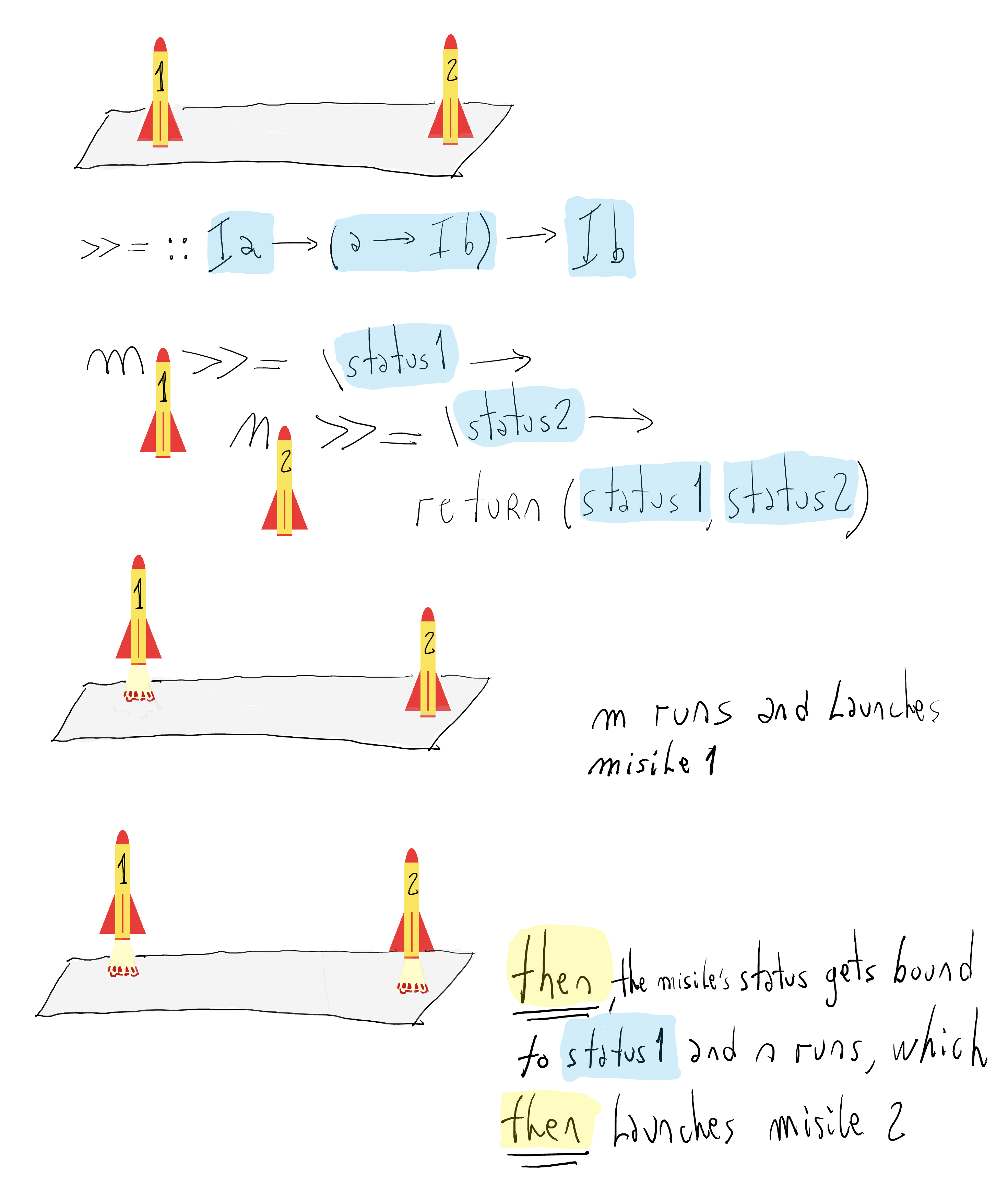The side-effects are sequentially executed!

Applicative code

The applicative structure does not impose an order on the execution of the container arguments. Observe that the effects could be run in parallel if possible.
Let's see the types closely

What is better? Monads, Applicative Functors?

FUNCTIONAL PEARL Applicative programming with effects by C. McBride and R. Paterson

The moral is this: if you’ve got an Applicative functor, that’s good; if you’ve also got a Monad, that’s even better! And the dual of the moral is this: if you want a Monad, that’s good; if you only want an Applicative functor, that’s even better!

Theory can prove that every monad is an applicative functor and that every applicative functor is a functor.
Exercise: Prove this, i.e.:
1. Given `instance Applicative m`, write a default `instance Functor m`. Prove the functor laws (assuming the applicative functor laws).
2. Given `instance Monad m`, write a default `instance Applicative m`. Prove the applicative functor laws (assuming the monad laws).
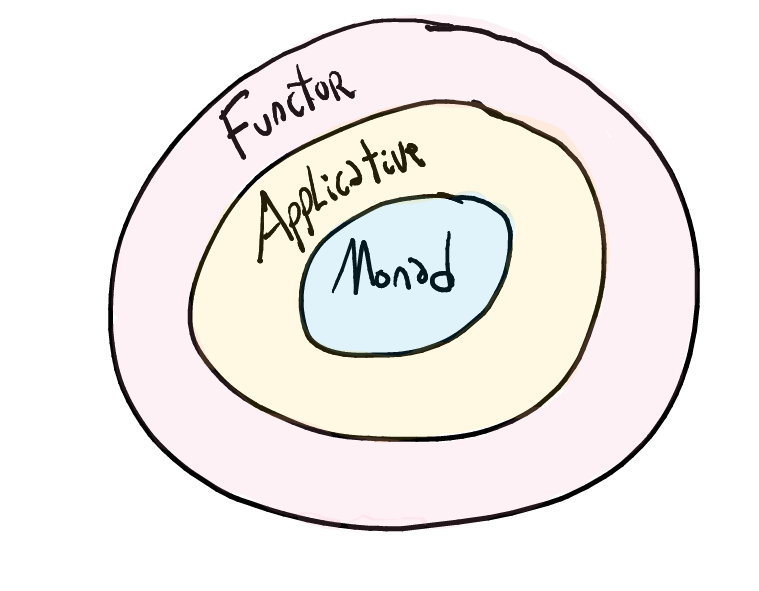
In Haskell, if you define a monad, i.e., give an instance of the type class Monad, you also need to give an instance of Applicative and Functor:
```
class Functor d     => Applicative d where
class Applicative d => Monad d       where
```
This requirement exists since GHC 7.10; for the rationale behind it, see the Functor-Applicative-Monad proposal.

Not a functor

Not every data type is a functor

type NotAFunctor = Equal
newtype Equal a = Equal {runEqual :: a -> a -> Bool}

fmapEqual :: (a -> b) -> Equal a -> Equal b
fmapEqual _f (Equal _op) = Equal \ _b1 _b2 -> error "Hopeless!"

What is the problem?

Values of type a are in "negative position", i.e., they are given to the function (not produced by it).

A functor, not applicative

Not every functor is applicative

data Pair r a = P r a

instance Functor (Pair r) where
    fmap f (P r a) = P r (f a)

Observe that the value of type r is kept as it is in the container (the functor does not create new elements, but modify existing ones)
If we want to create a container, we need an r but pure only receives an a
```
instance Applicative (Pair r) where
    P r1 f <*> P r2 a = P (r1 {- ?? Or r2 ? -}) (f a)
    pure x            = P (error "Hopeless!") x
```
Exercise: Is there a constraint C such that instance C => Applicative (Pair r) is definable? If yes, write out C and the instance!

Applicative, not a monad

Not every applicative functor is a monad
To show that, we need some preliminaries.
Every monoid is a phantom applicative functor
```
newtype Phantom o a =  Phantom o
```
Here, the type o is an element from a monoid. Roughly speaking, a monoid is a set of elements which contains a neutral element and an operation between the elements of such set.
```
mempty  :: o
mappend :: o -> o -> o
```
The neutral element has no effect on the result produced by mappend, i.e., mappend mempty o == o and mappend o mempty == o

We declare Phantom to be a functor and an applicative functor as follows.

instance Functor (Phantom o) where
   fmap f (Phantom o) = Phantom o

instance Monoid o => Applicative (Phantom o) where
   pure x                    = Phantom mempty
   Phantom o1 <*> Phantom o2 = Phantom (mappend o1 o2)

Observe that every application of <*> applies mappend.

To make this idea more concrete, let us define a concrete monoid: natural numbers.

data Nat = Zero | Suc Nat

instance Monoid Nat where
   mempty            = Zero
   mappend Zero    m = m
   mappend (Suc n) m = Suc (mappend n m)

Function mappend is simply addition.

Let us define the Phantom number one.

onePhantom :: Phantom Nat Int
onePhantom = Phantom (Suc Zero)

In some cases, when onePhantom is applied to an applicative function, it counts the total number of its occurrences.

(\ x y -> x) <$> onePhantom <*> onePhantom
> Phantom (Suc (Suc Zero))

Let us try to define Phantom Nat as a monad
```
instance Monad (Phantom Nat) where
  return = pure
```
The interesting case is (>>=)
```
Phantom n >>= k = ?
```
Observe that n :: Nat and k is waiting for an argument of type a and we have none! To make our instance type-checked, we ignore k.
```
Phanton n >>= k = Phanton m
    where m = ...
```
You are free to choose the m in the returned Phantom!

By the left identity rule for Monads, we have that
```
return x >>= k ≡ k x
```
By the definition of (>>=) above, we know that
```
return x >>= k ≡ Phantom m
```
By combining these two equations, we have that
```
Phantom m ≡ k x
```
Then, it is easy to come up with a function k where this equation does not hold. For instance,
```
k = \ _ -> ((\ x1 x2 .. xm xm1) -> x1) <$> onePhantom <*> .. <*> onePhantom
```
In other words, k is returning Phantom (Suc m) which is different from Phantom m. Contradiction! Therefore, Phantom Nat cannot be a monad.

List monad

Given f :: a -> b -> c, there are two generic ways to lift f to lists, getting [a] -> [b] -> [c].

Zipping ("pointwise"): zipWith f. This aligns the two lists and combines elements at the same index.
Cartesian product ("each with each"): cartesian f as bs = [ f a b | a <- as, b <- bs ].

Questions:

What are the units of these operations?
Can you formulate laws in the likeness of associativity?
With zipWith serving as liftA2 what would be the Applicative instance? Do the applicative functor laws hold?
With cartesian serving as liftM2 what would be the Monad instance? Do the monad laws hold?
(Hard:) Can you make a Monad where liftM2 = zipWith? Do the monad laws hold?

Exercise: Answer these questions and accompany your answers by proofs!

Structures learned so far

Monads
- Sequential construction of programs
- Useful to implement side-effects (e.g., error handling, logging, stateful computations, etc.).
  - Simplify code, i.e., it hides plumbing needed to handle the side-effects.
Applicative functors
- Useful to apply "multi-parameter" functions to multiple container arguments.
  - Simplify code, i.e., it hides the plumbing needed to take out functions and their arguments from containers, applying the function, and place the result back in a container.
- Side-effects could potentially be executed in parallel.
- They are more generic than monads.
Functors
- Useful to map functions into containers, i.e., transform data inside containers without breaking them.
  - Simplify code, i.e., it hides the plumbing of destructing the container to obtain the value, apply the function, and put the result in a container.
- The most general structure