Domain Specific Embedded Languages

A common problem in software development

Reading: DSL for the Uninitiated by Debasish Ghosh

Business users speak the domain terminology
- Stock market: bonds, stocks, options, etc.
- Cryptography: symmetric keys, asymmetric keys, games, perfect secrecy, chain blocked cypher, etc.
- Computer graphics: vectors, bézier curve, line, bézier spline, etc.
Developers speak software language
- Data types
- Functions
- Modules
- Lazy evaluation
There is a semantic gap.
How can we bridge the gap?
- Modeling the domain in software.
- In other words, we should aim to design a domain model in your software.
How do we start? What if the domain is colossal?
- Identify minimum domain model elements.
- Propose constructs that glue together domain model elements and create other (possible more complex) ones.
- Define how minimum and glued elements behave in your software.
The domain model elements and the corresponding constructs are the common language between the developer and the business users.
It is the domain specific language (or DSL) which brings the gap between business users and developers.

EDSL vs. DSL

What is the different between DSL and embedded DSL (or EDSL)?
A domain specific language can be provided as stand alone.
- You write a compiler/interpreter for the DSL and provide all the tools to program with it.
In contrast, an embedded DSL is written in a host language.
- It inherits the infrastructure (and programming language abstractions) of the host language.
- In this course, we use Haskell as the host language.
- We will leverage Haskell's
  - powerful type system,
  - generic programming features,
  - and tools
  for programming our DSL.
Many abstractions used in functional programming (e.g., monads) are known for being suitable to implement EDSLs. (We will see many examples along the course)

EDSL: Parts

EDSL Part	Description
Types	Model a concept
Constructors	Construct the simplest elements of such types
Combinators	Build complex elements from simpler ones
Run functions	Observe the EDSL elements, possibly producing side-effects when doing so

Let us get into a specific first in order to create a EDSL in Haskell.

Shapes: a simple EDSL for vectorial graphics

code

Design a language to describe vectorial graphics.
- Made of some basic shapes.
- They scale without loosing definition.
- Ideal for logos.
- Take less space as pixel-based formats (e.g., BMP, JPEG, etc.).

Types and constructors

We want to model simple graphics.

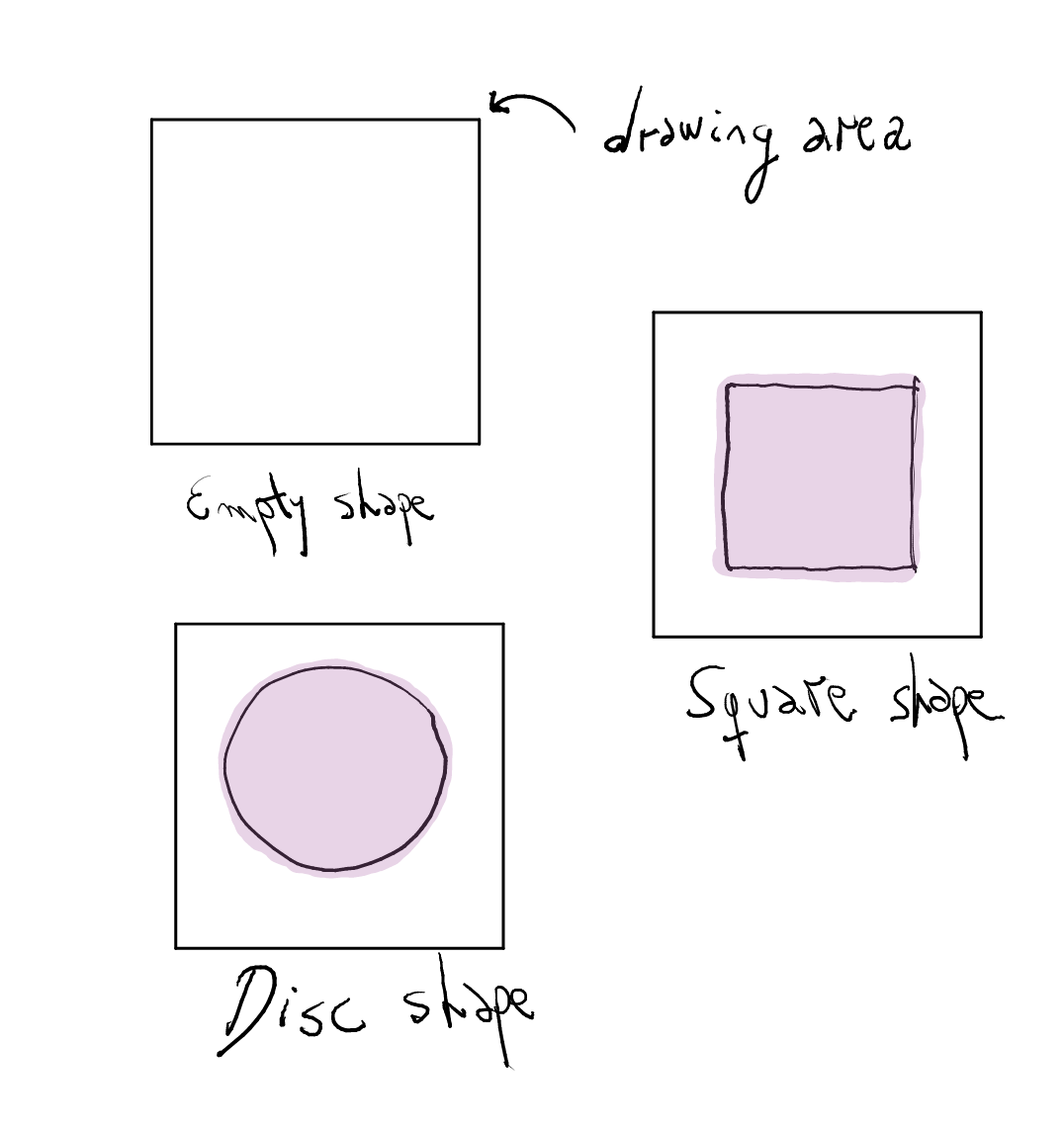
  data Shape
  empty  :: Shape
  disc   :: Shape
  square :: Shape

Some basic combinators

Let us visualize some useful combinators:

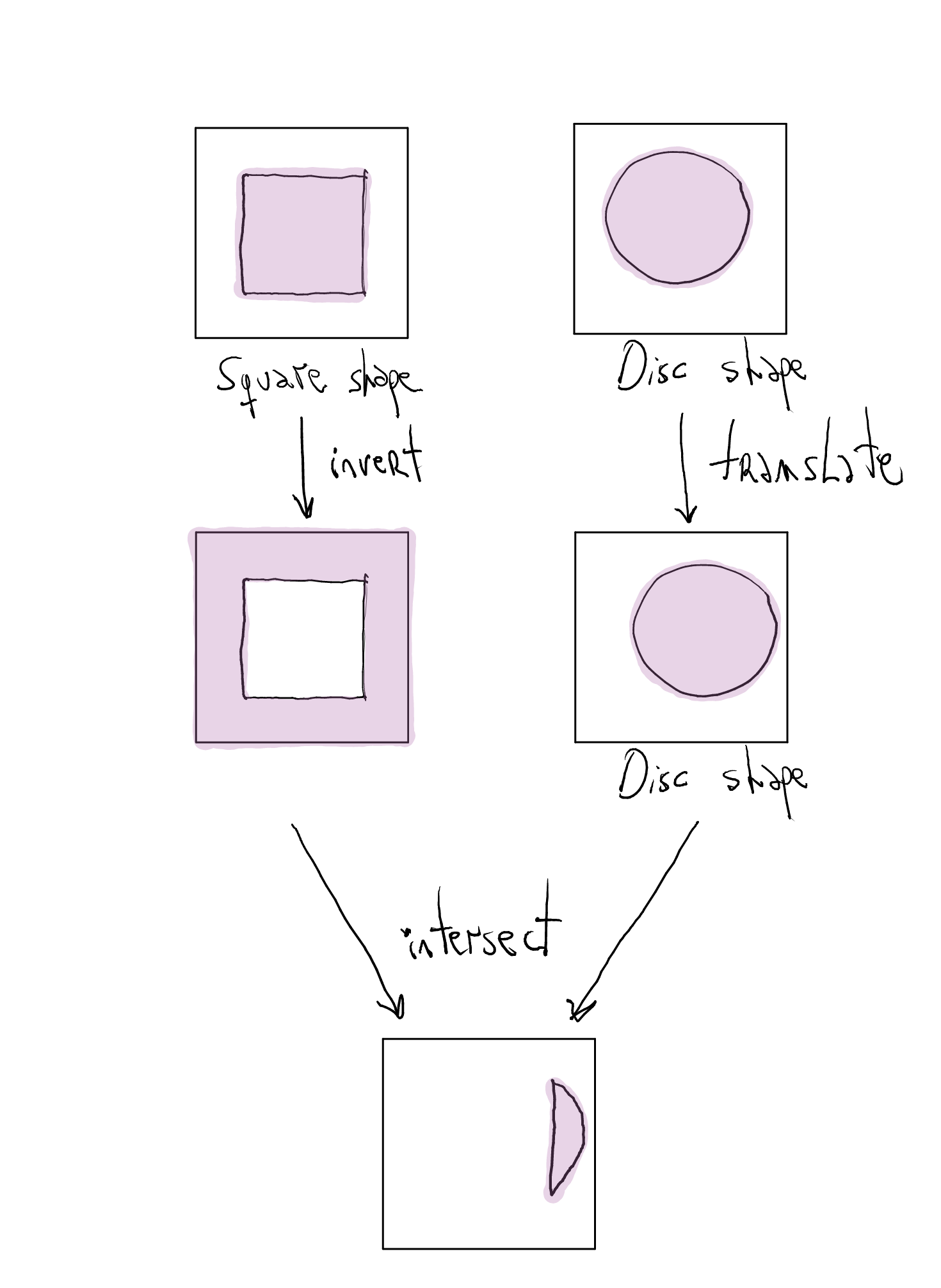
invert    :: Shape -> Shape
intersect :: Shape -> Shape -> Shape
translate :: ?

What about translate? We will move the figure based on a vector, i.e., on the x- and y-axes.
```
invert    :: Shape -> Shape
intersect :: Shape -> Shape -> Shape
translate :: Vec   -> Shape -> Shape
```
A new type (Vec) has appeared in the interface!

A run (observation) function

A raster is going to render the image
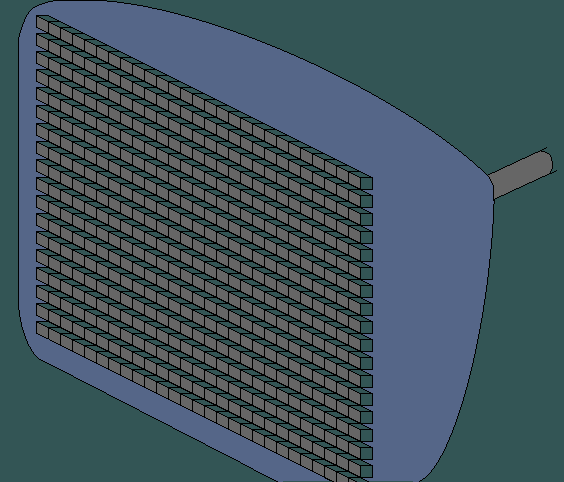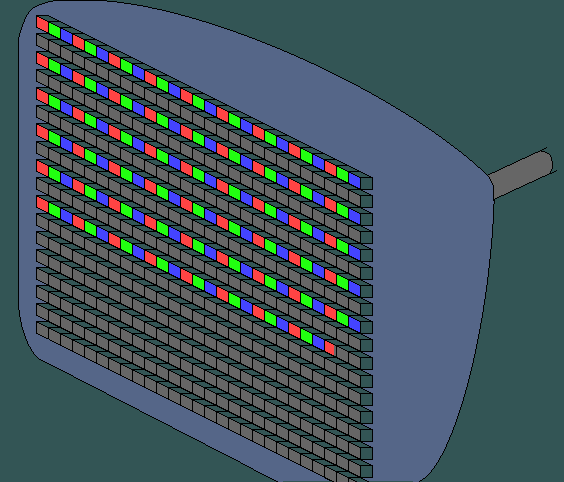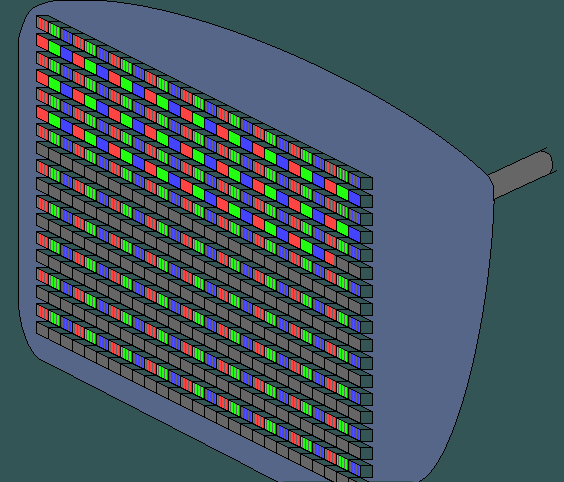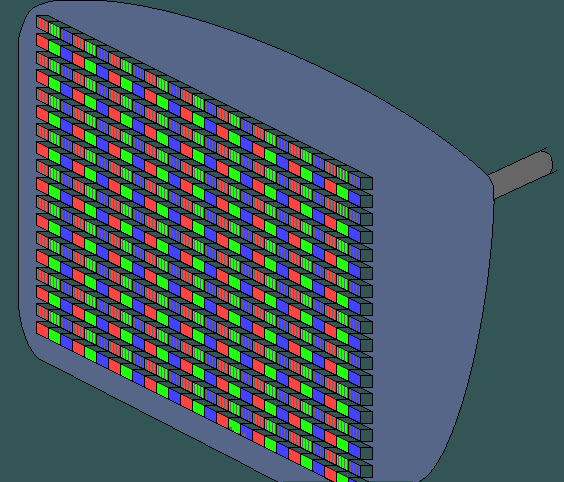
The raster is the one "observing" shapes and activating the corresponding pixels.
We assume the raster is composed of points (pixels if you wish).
```
inside :: Point -> Shape -> Bool
```
A new type (Point) has appeared in the interface!

Shapes: the interface

So far

newtype Shape

empty     :: Shape
disc      :: Shape
square    :: Shape
invert    :: Shape -> Shape
intersect :: Shape -> Shape -> Shape
translate :: Vec   -> Shape -> Shape
inside    :: Point -> Shape -> Bool

Aspects to think when designing an API
- Compositionality: combining elements into more complex ones should be easy and natural.
- Abstraction: the user should not have to know (or be allowed to exploit) the underlying implementation of your types.
Classification of operations
- A primitive operation is defined exploiting the definitions of the involved types.
- A derived operation is defined purely in terms of other operations.

Implementation: shallow embedding

Types: represent elements by their semantics, i.e., what they mean. It is usually done by leveraging some abstractions of the host language.
```
data Vec    = V { vecX, vecY :: Double }
data Point  = P { ptX,  ptY  :: Double }

newtype Shape = Shape (Point -> Bool)
```
In this case, we leverage Haskell functions!

Run functions: they are almost for free!

inside :: Point -> Shape -> Bool
p `inside` Shape sh = sh p

Constructor functions and combinators do most of the work.

 -- Constructors
 empty :: Shape
 empty = Shape \ _ -> False

 disc :: Shape
 disc = Shape \ p -> ptX p ^ 2 + ptY p ^ 2 <= 1

 square :: Shape
 square = Shape \ p -> abs (ptX p) <= 1 && abs (ptY p) <= 1

-- Combinators
invert :: Shape -> Shape
invert sh = Shape \ p -> not (inside p sh)

intersect :: Shape -> Shape -> Shape
intersect sh1 sh2 = Shape \ p -> inside p sh1 && inside p sh2

Translate deserves a bit of attention.

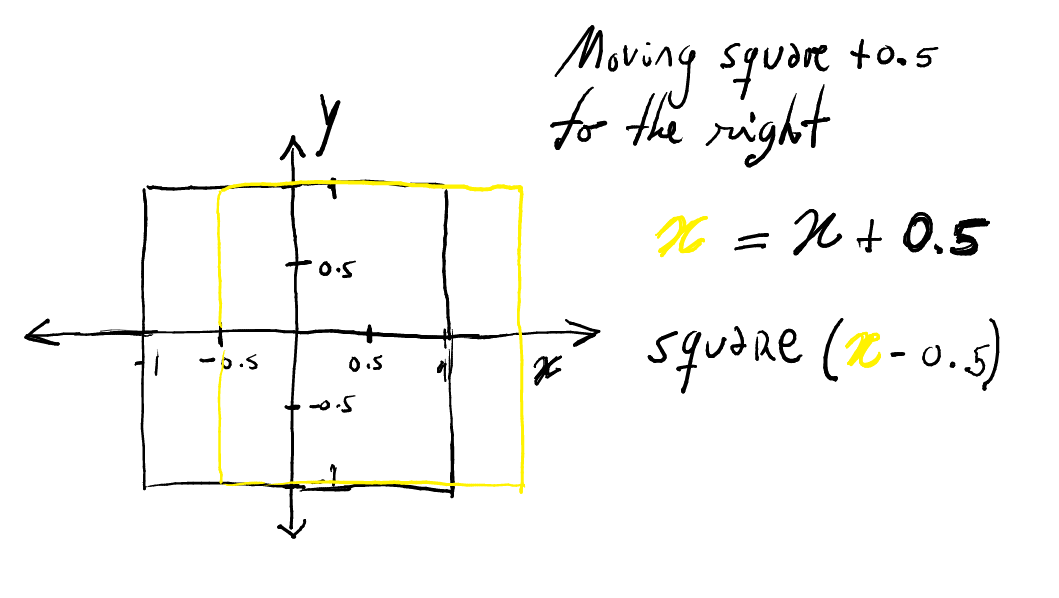
Observe that if a picture is moved n units to the left, then the characteristic functions should be applied to x - n instead.

sub :: Point -> Vec -> Point
sub (V x y) (V dx dy) = V (x - dx) (y - dy)

translate :: Vec -> Shape -> Shape
translate v sh = Shape \ p -> inside (p `sub` v) sh

Transformation matrices

Wikipedia

Basic idea
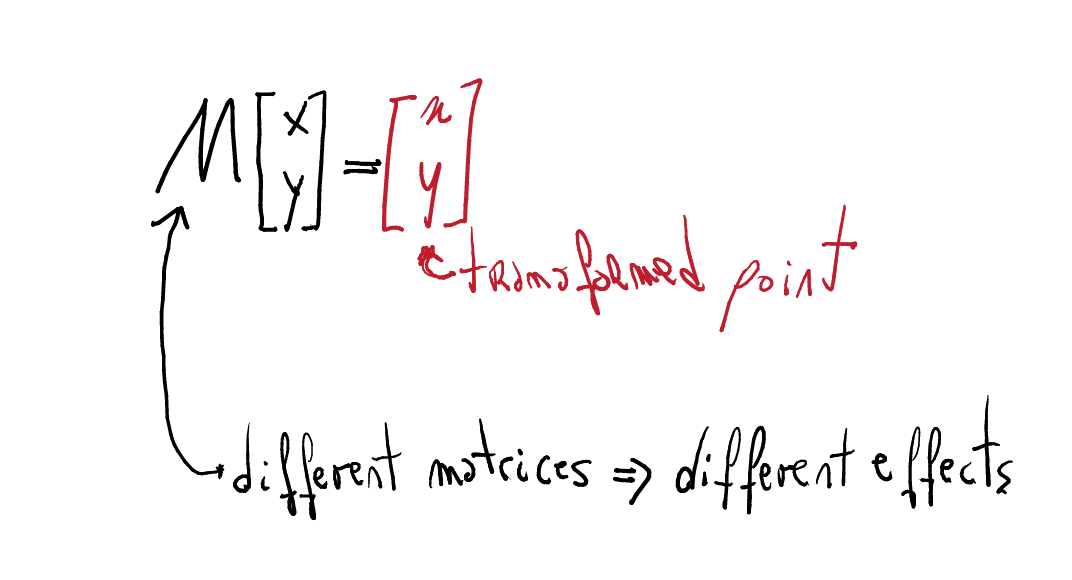
Let us see a concrete example: x-axis reflection:
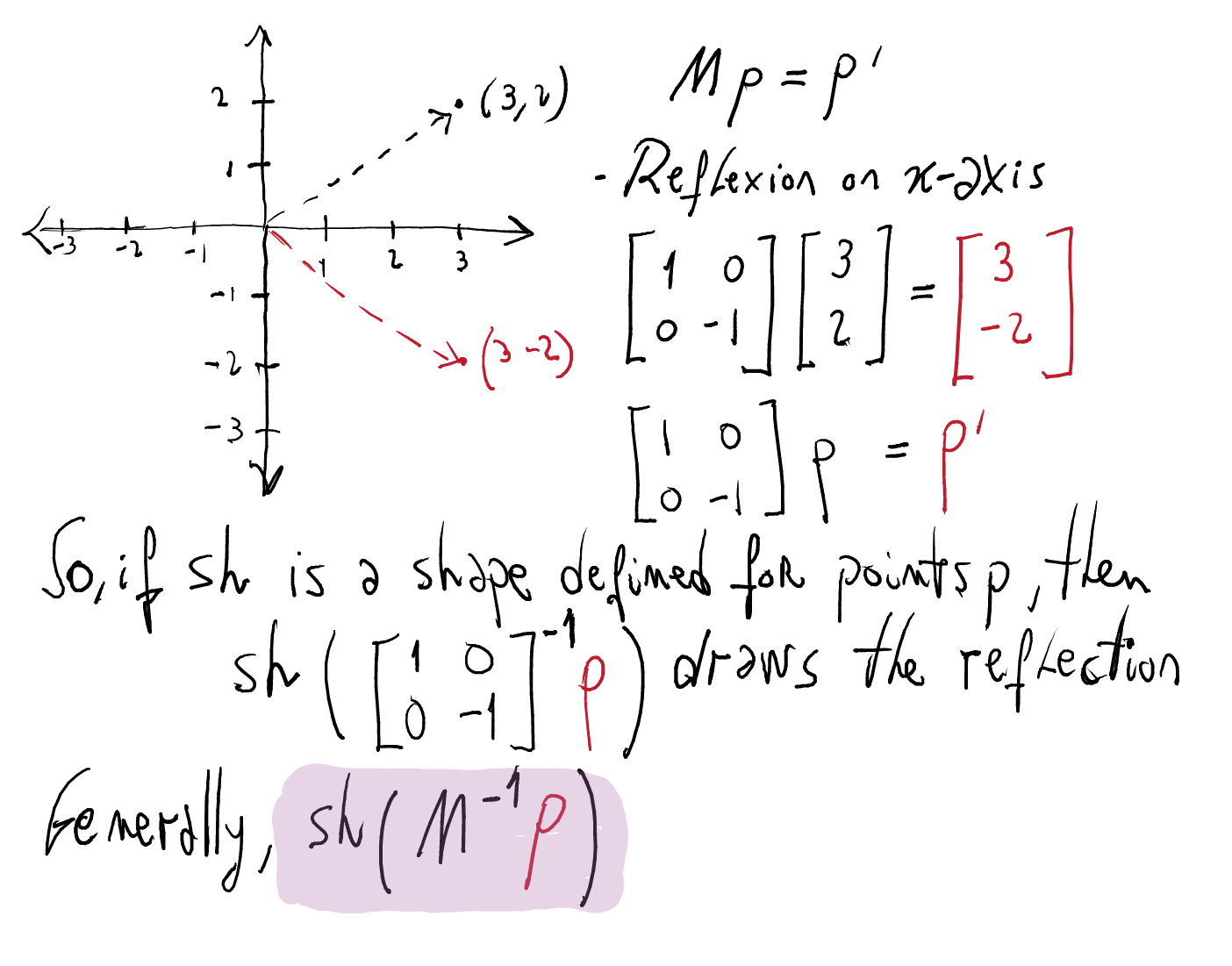
Observe that a point appearing in the "screen" depends if such point manipulated with some algebraic values appears in the considered shape.

We begin by introducing a new type for matrices and an inverse operation for them.

data Matrix = M { m00, m01, m10, m11 :: Double }

inv :: Matrix -> Matrix
inv (M a b c d)) = M (d / k) (-b / k) (-c / k) (a / k)
  where
    -- Determinant
    k = a * d - b * c

Now the transform operation:

transform :: Matrix -> Shape -> Shape
transform m sh = Shape \ p -> (inv_m `mul` p) `inside` sh
  where
    inv_m = inv m

Exercise: can you write the following derived operations?

-- reflects the shape on the x-axis
x-reflection :: Shape -> Shape

-- reflects the shape on the y-axis
y-reflection :: Shape -> Shape

-- Enlarge the shape by n% (n being the first argument)
zoom_in :: Int -> Shape -> Shape

Shape rotation

Axes rotation (math revisited):

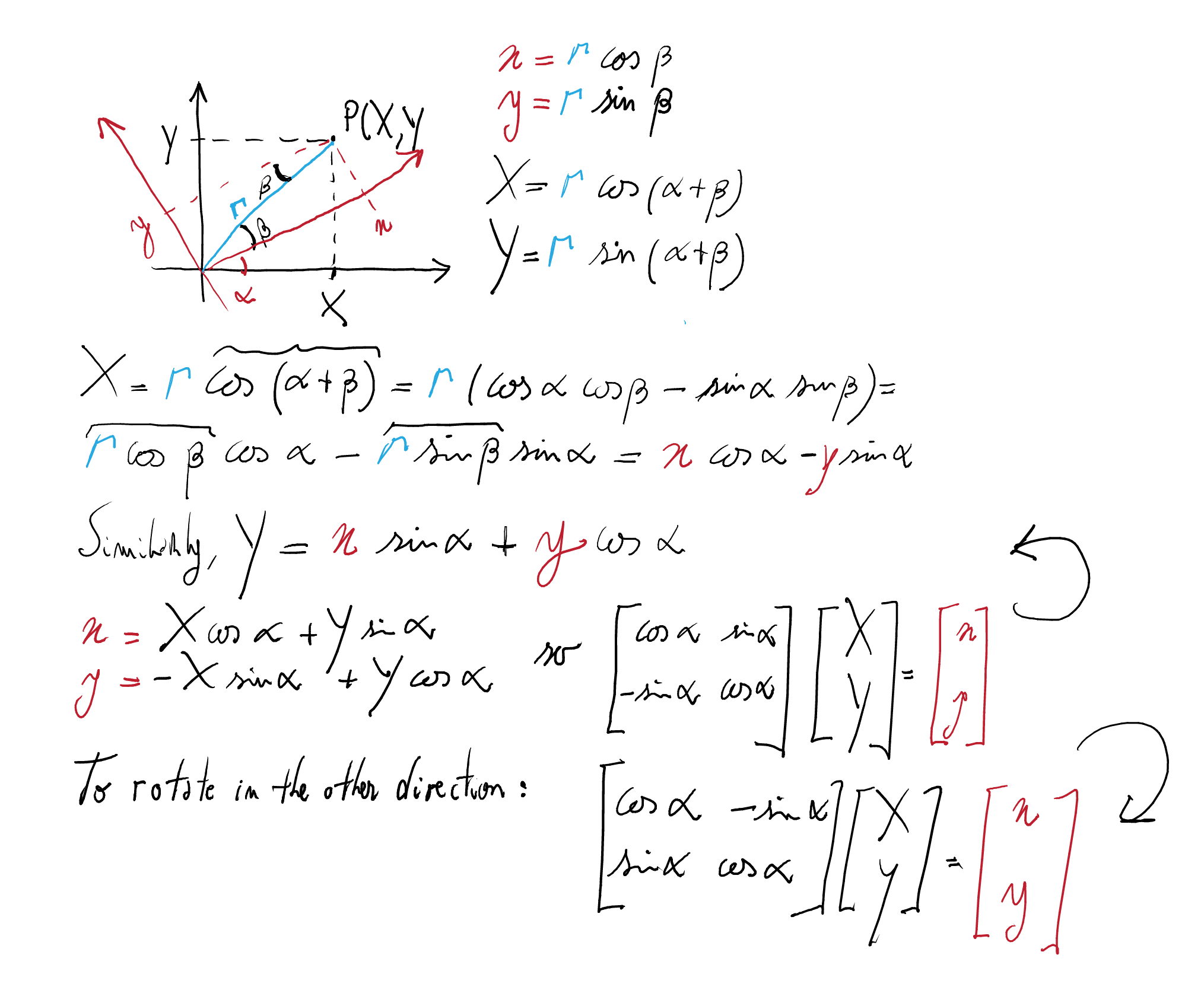
Which direction is the square shape rotated?

transform (m (pi/10)) square
  where
    m alpha = matrix
      (cos alpha)    (sin alpha)
      (-(sin alpha)) (cos alpha)

Clock-wise! Can you see why?

Points, Vectors, and Matrices in a separate module

The interface for shapes uses auxiliary mathematical abstractions.
We define them in a different module (Matrix.hs).

Alternative implementation: deep embedding

Types: represent how shapes are constructed (i.e., either by a basic shape or a combination of them).

data Shape where
  -- Constructor functions
  Empty   :: Shape
  Disc    :: Shape
  Square  :: Shape
  -- Combinators
  Translate :: Vec    -> Shape -> Shape
  Transform :: Matrix -> Shape -> Shape
  Intersect :: Shape  -> Shape -> Shape
  Invert    :: Shape  -> Shape

Constructors and combinators: almost for free! Simply map them into the appropriated constructors in the data type.

empty  :: Shape
empty  = Empty

disc   :: Shape
disc   = Disc

square :: Shape
square = Square

transform :: Matrix -> Shape -> Shape
transform = Transform

translate :: Vec -> Shape -> Shape
translate = Translate

intersect :: Shape -> Shape -> Shape
intersect = Intersect

invert :: Shape -> Shape
invert = Invert

Run (observation) function: all the work is here!

 inside :: Point -> Shape -> Bool
 _p `inside` Empty             = False
 p  `inside` Disc              = squaredDistance p <= 1
 p  `inside` Square            = maxNorm  p <= 1
 p  `inside` Translate v sh    = (p `sub` v) `inside` sh
 p  `inside` Transform m sh    = (inv m `mul` p) `inside` sh
 p  `inside` Union sh1 sh2     = p `inside` sh1 || p `inside` sh2
 p  `inside` Intersect sh1 sh2 = p `inside` sh1 && p `inside` sh2
 p  `inside` Invert sh         = not (p `inside` sh)

 -- * Helper functions
 squaredDistance :: Point -> Double
 squaredDistance p = x*x + y*y -- proper distance would use sqrt
   where
     x = ptX p
     y = ptY p

 maxNorm :: Point -> Double
 maxNorm p = max (abs x) (abs y)
   where
     x = ptX p
     y = ptY p

Shallow vs. Deep embedding

A shallow embedding (when it works out) is often more elegant and compact.
- Working out the type which provides the right semantics might be tricky.
A deep embedding is easier to extend.
- Adding new operations (by adding new constructors).
- Adding new run functions (e.g., inspection/debug printing).
- Adding optimizations (e.g., by data type manipulation).
Most of the time you get a mix between shallow and deep embedding.

In any case, abstraction is important!

module Shape.Shallow
(
  -- * Types
  Shape -- abstract
  -- * Constructor functions
, empty, disc, square
  -- * Primitive combinators
, transform, translate
, union, intersect, invert
  -- * Run functions
, inside
)
where ...

The interface should not change based on a shallow or deep embedding implementation! No difference for the user of the EDSL!

Rendering a shape to ASCII-art

A very interesting run function!

It introduces the concept of windows.

defaultWindow :: Window
defaultWindow = Window
  { bottomLeft           = point (-1.5) (-1.5)
  , topRight             = point 1.5 1.5
  , horizontalResolution = 40
  , verticalResolution   = 40
  }

It has a dimension in terms of characters.
It has a dimension in terms of points.

The render function essentially maps points to characters in a window.

-- | Generate a list of evenly spaced (n :: Int) points in an interval.
samples :: Double -> Double -> Int -> [Double]

-- | Generate the matrix of points corresponding to the pixels of a window.
pixels :: Window -> [[Point]]

-- | Render a shape in a given window.
render :: Window -> Shape -> String
render win sh = unlines $ map (concatMap putPixel) (pixels win)
  where
    putPixel p  | p `inside` sh = "[]"
                | otherwise     = "  "

Function unlines and concatMap are standard.

Discussion

Adding colored shapes:
- Discuss what you need to do!
Bad shallow implementations:
- Looking at the render run function, we might decide to go for:
```
newtype Shape = Shape (Window -> String)
```
- Discuss the problem with this implementation.
Other questions/comments?

Signal: Another EDSL

We are interested to produce animated shapes.
For that, we need to model how they might change based on time.
We take inspiration from functional reactive programming approaches.
We introduce the concept of Signal, a value that changes over time.
More specifically, we have the following initial API for our new EDSL.
```
-- Constructors
constS :: a -> Signal a
timeS  :: Signal Time
-- Combinators
applyS :: Signal (a -> b) -> Signal a -> Signal b
-- Run function
sample :: Signal a -> Time -> a
```
- Function constS produces a constant value, i.e., it does not change with time.
- Function timeS reveals the current time, i.e., it is a signal which arrives at time t and produces the value t.
- Combinator applyS takes a functional signal and converts it into a function which changes Signal a into Signal b.
- Run function sample just extracts the meaning of a signal.

How do we program with it?

code

Let us try to get the next simple animation:

We write time-dependent functions which generate shapes.

A function for intermittently displaying two shapes:

-- | It displays a shape on "odd times" and another one in "even times".
change :: Shape -> Shape -> Time -> Shape
change sh1 sh2 t
  | odd (floor t) = sh1
  | otherwise     = sh2

Convert them into signals:

  constS (change disc square) :: Signal (Time -> Shape)

Convert the functional signal into a signal (corresponding to the image of the function) by applying time information. How do get time information? We use timeS!
```
  square_disc = constS (change disc square) `applyS` timeS
  
```

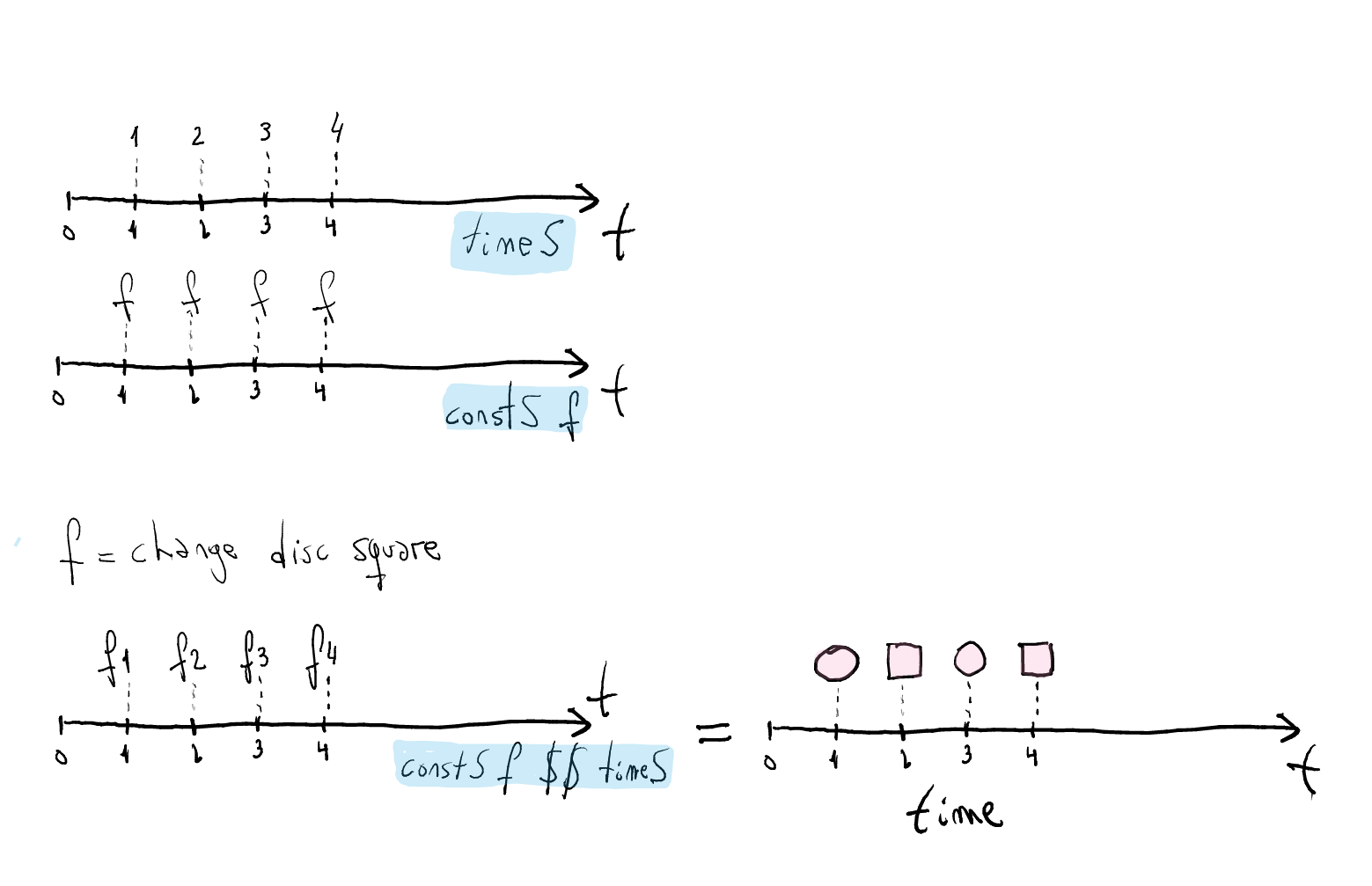
In general: create a Signal from a Time-varied value:

signal :: (Time -> a) -> Signal a
signal f = constS f `applyS` timeS

square_disc = signal (change disc square)

More operations

We will consider two more operations

-- Combinator
mapT   :: (Time -> Time) -> Signal a -> Signal a
-- Derived operation
mapS   :: (a -> b) -> Signal a -> Signal b

Combinator mapT allows to alter the mapping among Time and Shape.

to_zero :: Time -> Time
to_zero = const 0

always_square :: Signal Shape
always_square = mapT to_zero square_disc

Exercise: write mapS as a derived operation!

Implementation: shallow embedding

We will model signals as Haskell functions of time Time -> a.

type Time = Double
newtype Signal a = Sig { sample :: Time -> a }

constS :: a -> Signal a
constS x = Sig (const x)

timeS :: Signal Time
timeS = Sig id

applyS :: Signal (a -> b) -> Signal a -> Signal b
fs `applyS` xs = Sig (\ t -> sample fs t (sample xs t))

mapT :: (Time -> Time) -> Signal a -> Signal a
mapT f xs = Sig (sample xs . f)

sample :: Signal a -> Time -> a

signal :: (Time -> a) -> Signal a
signal = Sig

Implementation: deep embedding

type Time = Double
data Signal a where
  ConstS :: a -> Signal a
  TimeS  :: Signal Time
  MapT   :: (Time -> Time) -> Signal a -> Signal a
  ApplyS :: Signal (a -> b) -> Signal a -> Signal b

constS = ConstS
timeS  = TimeS
...

The run function generates the functions of type Time -> a (most of the work is here!).

-- | Sampling a signal at a given time point.
sample (ConstS x)     = const x
sample TimeS          = id
sample (ApplyS fs xs) = \ t -> sample fs t (sample xs t)
sample (MapT f xs)    = sample xs . f

Go live!

code

Summary

Different kind of operations
- Constructors, combinators, and run functions
- Primive or derived operations
Implementation styles
- Shallow embedding: representation given by semantics
- Deep embedding: representation given by operations
Remember
- Compositionality
- Abstraction