Introduction to the course

This course

Advanced Programming Language Features
- Type systems
- Programming techniques
- Program calculation and equational reasoning
In the context of Functional Programming
- Haskell
- Agda
Applications
- Signals processing, graphics, web programming, security
- Domain Specific Languages

Self study

You need to read yourself
Find out information yourself
Solve problems yourself
With (a lot of) help from us!

Getting help

Course homepage
- It should be comprehensive -- complain if it is not!
Discussion board
- Discuss general topics, find lab partner, etc.
- Don't post (partial or complete) lab solutions
Office hours
- A few times a week. Check the hours here.
Send e-mails to teachers (myself and the assistants)
- Organizational help, lectures, etc. (Lecturer)
- Specific help with programming labs (Assistants)

Organization

2 Lectures per week
- Including a few guest lectures
- Two exercise sessions (we solve, for example, previous exams)
3 Programming assignments (labs)
- Done in pairs (use the discussion groups to pair up)
- No scheduled lab supervision (use the office hours instead!)
1 Written exam
**Final grade: 60% labs + 40% exam**

Recalling Haskell

Purely functional language
- Functions vs. actions
- Referential transparency
Lazy evaluation
- Things are evaluated when needed and at most once
Advanced (always evolving) type system
- Polymorphism
- Type classes
- Type families
- etc.
Quiz menti.com 8725 3240: What is the result of ensurePrime 4?
1. error "not prime"
2. 4
3. non-termination

Functions vs. Actions

Consider
```
f :: String -> Int
```
Only the knowledge about the string is needed to produce the result. We say that f is a pure function.
What about external input and output?
Haskell has a distinctive feature with respect to other programming languages:

Pure code is separated from that which could affect the external world!
How?

Types!
Code which has side-effects in the real world has type IO a (for some a).
```
g :: String -> IO Int
```
As f, this function produces an action which, when executed, produces an integer. However, it might
- use anything to produce it, e.g., data found in files, user input, randomness, and
- modify anything, e.g., files, send packages over the network, etc.

Programming with `IO`

code

Interacting with the user:

hello :: IO ()
hello = do
  putStrLn "Hello! What is your name?"
  name <- getLine
  putStrLn $ "Hi, " ++ name ++ "!"

A program that enumerates and prints a list of strings:

> printTable ["1g saffran", "1kg (17dl) vetemjöl", "5dl mjölk",
              "250g mager kesella", "50g jäst", "1.5dl socker",
              "0.5tsk salt"]
1: 1g saffran
2: 1kg (17dl) vetemjöl
3: 5dl mjölk
4: 250g mager kesella
5: 50g jäst
6: 1.5dl socker
7: 0.5tsk salt
>

printTable :: [String] -> IO ()
printTable = prnt 1  -- Note the use of partial application
  where
    prnt :: Int -> [String] -> IO ()
    prnt _i []       = return ()
    prnt  i (x : xs) = do
      putStrLn $ show i ++ ": " ++ x
      prnt (i + 1) xs

IO actions are first class, i.e., you can pass them around and store them as any other value.
Can we write printTable differently?

Let us create a list of actions and then sequentially show them.

printTable2 :: [String] -> IO ()
printTable2 xs =
  sequence_ [ putStrLn $ show i ++ ":" ++ x
            | (x, i) <- xs `zip` [1 .. length xs]
            ]

sequence_ :: [IO ()] -> IO () -- Prelude

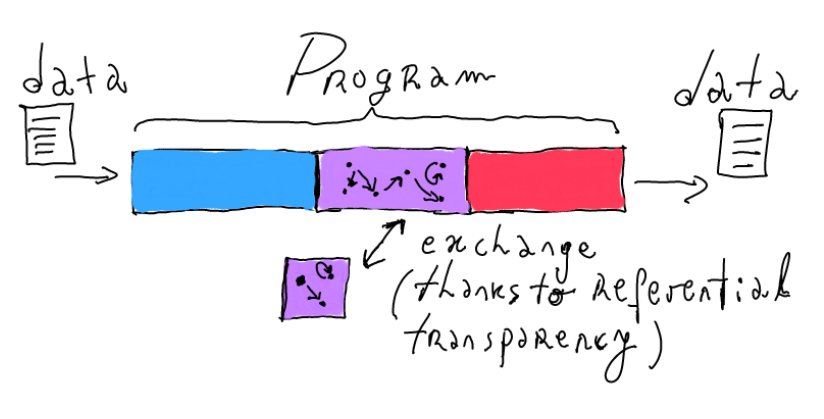
Referential transparency

Quiz menti.com 8725 3240: In which languages (if any) does the distributive law (x + y) * f() = x * f() + y * f() hold?
- Haskell
- Java
- Python
What is it? "...An expression may contain certain 'names' which stand for unknown quantities, but it is normal in mathematical notation to presume that different occurrences of the same name refer to the same unknown quantity... "

"...the meaning of an expression is its value and there are no other effects, hidden or otherwise, in any procedure for actually obtaining it. Furthermore, the value of an expression depends only on the values of its constituent expressions (if any)..."

Source: R. Bird and P. Wadler, Introduction to Functional Programming, 1st edition, Section 1.2, page 4
What does it buy us?
- Equational reasoning, i.e., expressions can be freely changed by others that denote the same value.
- Example associativity of the append function:
```
(xs ++ ys) ++ zs = xs ++ (ys ++ zs)
```
What about programs with I/O?
- In Haskell, expressions of type IO a (for some type a) are pure expressions which denote (describe) I/O actions.
- In other words, an expression of type IO a is not the computation itself but rather a pure description of it.
- This enable us to also do equational reasoning on IO actions.
- Unfortunately, we do not always have the definition of the functions describing I/O effects (e.g., putStrLn, getLine, etc.). Nevertheless, we can still do some reasoning based on the underlying structure of IO (monad). For instance, the code
```
do putStrLn "Hi!"
   name <- getLine
   return $ "hi! " ++ name
```
  is equivalent to
```
do putStrLn "Hi!"
   name <- getLine
   return 42
   return $ "hi! " ++ name
```

Referential transparency in practice

In practice, changing expressions by others denoting the same values might have consequences in:
- memory and energy consumption
- performance
Evaluation of expressions often trigger a lot of side-effects (memory allocation, garbage collector, etc.) even though they are pure.

That expressions denote the same value does not mean that they are equally convenient to use in practice!

Evaluation orders

Eager evaluation

Most programming language use this strategy: ML (OCaml), Java, Python...

Variables are bound to values, not expressions. So, function arguments are reduced to values before calling the function.

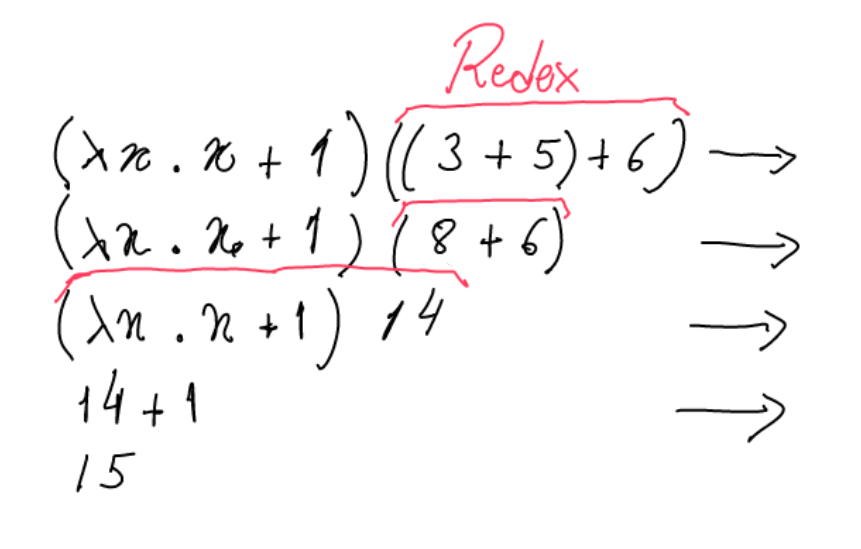
Eager evaluation
Programmer dictates the execution order by the structure of their code.
The runtime overhead is usually small.
It promotes early error propagation.
Evaluation of unnecessary expressions.
Programmers need to organize the code for optimal execution based on the reduction order.

Lazy evaluation
- Haskell is a lazy language.
- Expressions are evaluated only when needed.
- Expressions are evaluated at most once.
  
  (We will explore more in detail what this means.)

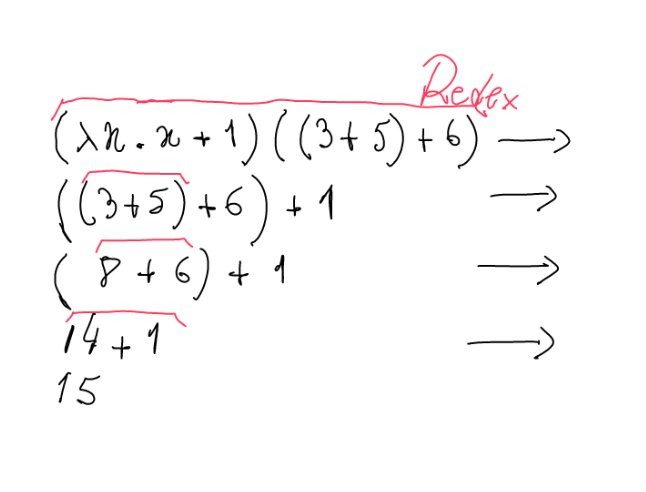
Observing evaluations in Haskell

Use error "message" or undefined to see whether something gets evaluated.

testLazy2 = head [3, undefined, 17]
testLazy3 = head (3 : 4 : error "no tail")
testLazy4 = head [error "no first elem", 17, 13]
testLazy5 = head (error "no list at all")

Lazy evaluation: skipping unnecessary computations

Consider the following functions

-- | Fibonacci
expn :: Integer -> Integer
expn n | n <= 1    = 1
       | otherwise = expn (n-1) + expn (n-2)

choice :: Bool -> a -> a -> a
choice False  f  _t  =  f
choice True   _f  t  =  t

Function expn is "expensive" to compute. Do you see why?

What does happen when running...?

testChoice1 :: Integer
testChoice1 = choice False 17 (expn 99)

testChoice2 :: Integer
testChoice2 = choice False 17 (error "Don't touch me!")

Lazy evaluation: programming style

Programs separate the
- construction
- and selection of data for a given purpose.
Modularity: "It makes it practical to modularise a program as a generator which constructs a large number of possible answers, and a selector which chooses the appropriate one."

Why Functional Programming Matters by John Hughes

Lazy evaluation: when is a value "needed"?

An argument is evaluated when a pattern match occurs

strange :: Bool -> Integer
strange False = 17
strange True  = 17

testStrange = strange undefined

Primitive functions also evaluate their arguments.

Lazy evaluation: at most once?

ff :: Integer -> Integer
ff x = (x - 2) * 10

foo :: Integer -> Integer
foo x = ff x + ff x

bar :: Integer -> Integer -> Integer
bar x y = ff 17 + x + y

testBar = bar 1 2 + bar 3 4

ff x gets evaluated twice in foo x.
ff 17 is evaluated twice in testBar.
Why is that?
In lazy evaluation, bindings are evaluated at most once!
- We can adapt foo above to evaluate ff x at most once by introducing a local binding:
```
foo :: Integer -> Integer
foo x = ffx + ffx
  where ffx = ff x
```
- The evaluation happens at most once in the corresponding scope!
- What about f 17? How can we change bar to evaluate it at most once?
```
bar :: Integer -> Integer -> Integer
bar = \ x y -> ff17 + x + y
  where
    ff17 :: Integer
    ff17 = ff 17
```
  We introduce a binding ff17 that can be evaluated before the function arguments are passed.

Lazy evaluation: infinite lists

Because of laziness, Haskell is able to denote infinite structures.
They are not computed completely!
Instead, Haskell only computes the needed parts from them.
Infinite lists examples:
```
take n [3..]
xs `zip` [1..]
```

We can write "generic code" which gets "instantiated" to the appropriate case.

printTable3 :: [String] -> IO ()
printTable3 xs =
  sequence_ [ putStrLn $ show i ++ ":" ++ x
            | (x, i) <- xs `zip` [1..]
            ]
testTable3 = printTable3 lussekatter

Observe that zip takes an infinite list [1..] but it will only use length xs many elements.

Other examples

Raising functions to a positive power:

iterate :: (a -> a) -> a -> [a]
iterate f x = x : iterate f (f x)

> iterate (2*) 1
[1,2,4,8,16,32,64,128,256,512,1024,...]

Repeating an element infinitely:

repeat :: a -> [a]
repeat x = x : repeat x

Creating periodic lists:

cycle :: [a] -> [a]
cycle xs = xs ++ cycle xs

Alternative, non-recursive definitions:

repeat :: a -> [a]
repeat = iterate id

cycle :: [a] -> [a]
cycle xs = concat (repeat xs)

Lazy evaluation: infinite lists exercises

Problem: let us define the function

replicate :: Int -> a -> [a]
replicate = ?

such that

> replicate 5 'a'
"aaaaa"

replicate :: Int -> a -> [a]
replicate n x = take n (repeat x)

Problem: grouping lists elements into lists of equal size.

chunksOf :: Int -> [a] -> [[a]]
chunksOf = ?

> chunksOf 4 "thisthatok!"
["this", "that", "ok!"]
> chunksOf 4 "thisthatok!!"
["this", "that", "ok!!"]

chunksOf n = takeWhile (not . null)
           . map (take n)
           . iterate (drop n)

Function composition (.) connects data processing "stages" -- like Unix pipes!

Problem: prime numbers

primes :: [Integer]
primes = ?

> take 4 primes
[2,3,5,7]

primes :: [Integer]
primes = sieve [2..]
  where
    sieve (p : xs) = p : sieve [ y | y <- xs, y `mod` p /= 0 ]
    sieve []       = error "sieve: empty list is impossible"

This algorithm is commonly mistaken for Eratosthenes' sieve -- see that paper The Genuine Sieve of Eratosthenes for more details.

Lazy evaluation: infinite data structures

Consider the following data structure:

data Labyrinth = Crossroad
  { what  :: String
  , left  :: Labyrinth
  , right :: Labyrinth
  }

Let us define a labyrinth.

labyrinth :: Labyrinth
labyrinth = start
  where
    start  = Crossroad "start"  forest town
    town   = Crossroad "town"   start  forest
    forest = Crossroad "forest" town   exit
    exit   = Crossroad "exit"   exit   exit

What does it happen when we print out labyrinth?

Lazy evaluation: conclusions

Lazy evaluation
Avoids unnecessary computations (a different programming style).
Provides error recovery.
Allows to describe infinity data structures.
Can make programs more modular.
Makes complexity analysis hard.
Is not suitable for time-critical operations.

Type classes