Type-based modeling & looking back!

Type-based modeling

In this lecture, we will see some advanced type-system features for Haskell
Most advanced type-system features are introduced for two purposes
- Typing more well-behaved programs
- Typing less bad-behaved programs

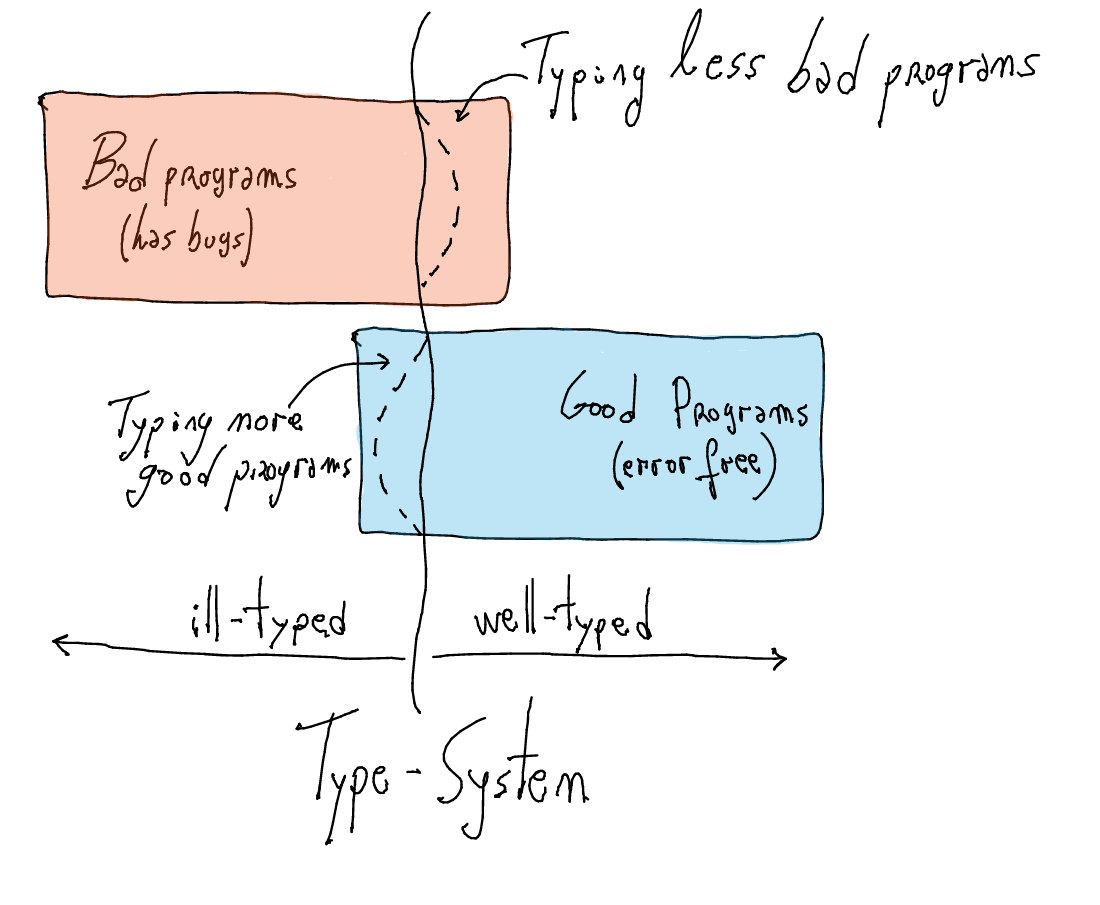
Typing more well-behaved programs

In Haskell, the addition has the following signature
```
(+) :: Num a => a -> a -> a 
```
This allows any numeric type to be used for addition as long as both arguments have the same type.
In math, it is common to allow addition of, for example, integers and real numbers.
Defining a more flexible addition is a nice little exercise to introduce associated types (type families).
In principle, there is no reason for not typing the following expression
```
(1 :: Int) + (2.5 :: Float) 
```
A good implementation for "this" (+) requires to "cast" the left-side argument to a float and then perform the sum.

Associated types

What is the type of (+)?

(1 :: Int) + (2.5 :: Float)

In this case, we have that

(+) :: Int -> Float -> Float

If we have other arguments,

(1.5 :: Double) + (2.1 :: Float)

Then, we have that

(+) :: Double -> Float -> Double

The resulting type of (+) depends on the type of the arguments.

When there are dependencies, there are chances to use functions!

If you think F as a function on types, we can give the type signature of (+) as follows.
```
(+) :: a -> b -> F a b 
```

An associate type is a function at the level of types

 class Add a b where        -- uses MultiParamTypeClasses
   type F a b               -- uses TypeFamilies as well
   add :: a -> b -> F a b

Roughly speaking, functions at the type level require the TypeFamilies extension.

Where do we give the definition of F?

In the type class instances!

instance Add Integer Double where
  type F Integer Double = Double  -- defining F
  add x y = fromIntegral x + y

instance Add Double Integer where
  type F Double Integer = Double  -- defining F
  add x y = x + fromIntegral y

As for (+), we define add for arguments of the same type.

instance (Num a) => Add a a where -- uses FlexibleInstances
  type F a a = a
  add x y = x + y

We can even define addition between a number and a list (of integer, float, etc.).

instance (Add Integer a) =>
         Add Integer [a] where    -- uses FlexibleContexts
  type F Integer [a] = [F Integer a]
  add x ys = map (add x) ys

Now, we can safely add elements of different types

test = add (3::Integer) (4::Double)

aList :: [Integer]
aList =  [0,6,2,7]

test2 :: [Integer]
test2 = add (1::Integer) aList

test3 :: [Double]
test3 = add (38::Integer) [1700::Double]

Typing less bad-behaved programs

Type-systems are not perfect!

We can still write well-typed programs which fail at runtime. They do not fail due to a type-error, but rather a problem in its semantics.

Type-systems *ensure that no type-error are raised at runtime*, but they do not say anything about other type of errors programs might have
```
> head []
*** Exception: Prelude.head: empty list

> [1,2,3] !! 5
*** Exception: Prelude.(!!): index too large 
```
We would like our type-system to help us out to rule out such programs
For that, we are going to encode more of our functions invariants into the types.

For instance, in the example above, the type of a list indicates its length.
```
[1,2,3] :: Vector 3 Int 
```
Having the length as part of the type, we can now impose a restriction on the function accessing to elements of a list.
```
(!!) :: (n <= m) => Vector n Int -> m -> Int
```
Haskell does not have a strong enough type-system (e.g., like Agda) to encode the type of lists and (!!) exactly as described above. However, we will get very "similar" types by using several extensions.

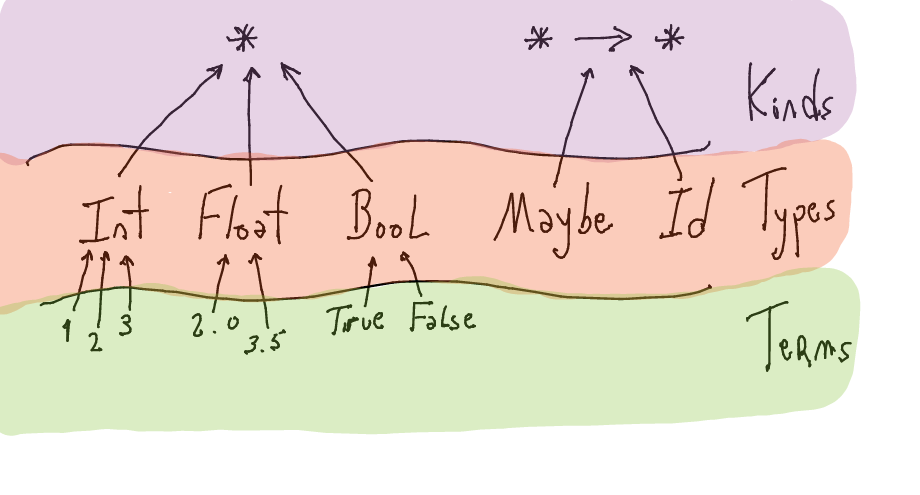
Kinds

Kinds are the type of types

Haskell has the kind *, the type of all the types

Int  :: *
Bool :: *
Char :: *
Char -> Bool :: *
(Char, Bool) :: *

What about type operators? (e.g., Maybe, [])

A type operator is essentially a type-level constructor which generates a type based on its argument(s).
```
Maybe :: * -> *
[]    :: * -> *
(->)  :: * -> * -> *
```
The kind of type operators describes the amount of type arguments required to produce a type. For instance, Maybe is waiting for a single type, so Maybe Bool :: * produces a type for optional boolean values. Similarly, (->) a b :: * produces the type of functions going from a to b.

Revisiting monad transformers, we have that
```
StateT :: * -> (* -> *) -> * -> * 
```
Observe that the second kind argument is a type constructor, i.e., the monad to apply the transformer.
Kinds take us one level up in the organization of Haskell's abstractions

Data kinds

To express invariants at the level of types, we would like to talk about values as types.

For instance,
```
(!!) :: m <= n => ... 
```
We are thinking about the values m and n as types instead.
The extension DataKinds automatically promotes every suitable datatype to be a kind and its constructors to be types/type constructors.
Let us take as an example natural numbers
```
data Nat where
     Zero :: Nat
     Suc  :: Nat -> Nat 
```
With DataKinds, we have the following kinds and types/type constructors (with no inhabitants but undefined).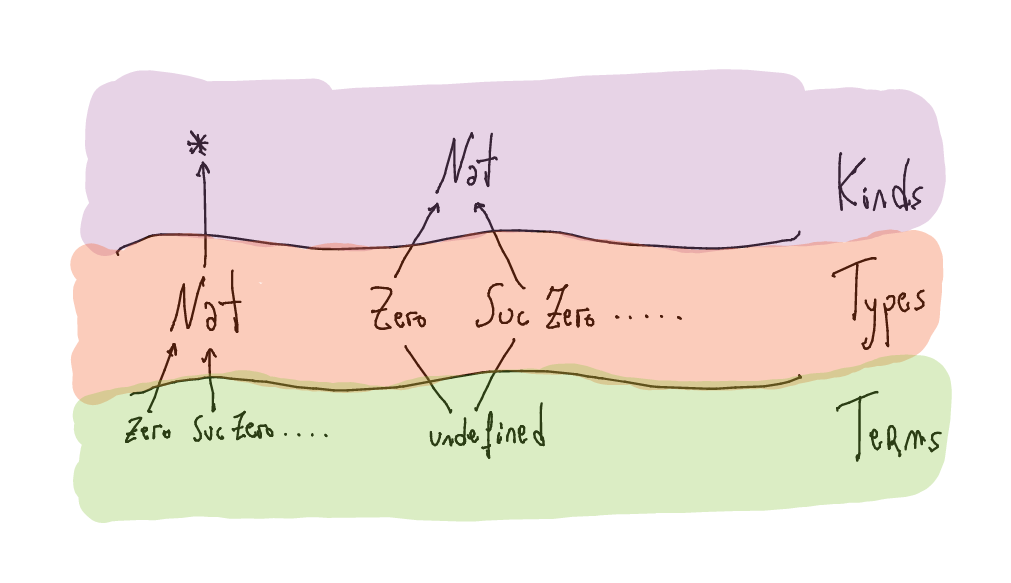

Once we have kinds, we can use them to restrict the types used in a GADT. In our example, we are going to denote the length of a vector with a type-level natural.
```
data Vector a (n :: Nat) where   -- uses KindSignatures
  Nil  :: Vector a Zero
  (:-) :: a -> Vector a n -> Vector a (Suc n) 
```
Now, we can write
```
array :: Vector Int (Suc (Suc Zero))
array = 2 :- (1 :- Nil) 
```
Observe that we cannot write an array which length is not properly captured by the types. The following expressions are ill-typed.
```
array2 :: Vector Int (Suc (Suc Zero))
array2 = (1 :- Nil) 
```
By using the data kind `Nat` in the GADT, we capture the length of lists in the types!

We are going to keep this fact as an invariant for every built vector.

Type families

What if we need to append two existing arrays? What is the length of the resulting data?
We need to compute its length at the type-level, i.e., at compile time!
```
append :: Vector n a -> Vector m a -> Vector a ? 
```
Which type should I use? Clearly, it should be the type that represents the "sum" of types n and m.

We would like to compute the length (type) of the resulting array as a function on the types n and m.
```
append :: Vector n a -> Vector m a -> Vector a (Sum n m) 
```
Function Sum needs to get evaluated at compile-time!

Instead of using Sum, we can use more fancy notation.
```
append :: Vector n a -> Vector m a -> Vector a (n :+: m) 
```
How can we define such type-level functions?
Type families are type-level functions, which come in two flavors (opened and closed)
In this course, we are going to use closed typed families
A type family is closed when all its equations are given in the same module. It is then easier for GHC to manipulate them -- it does not need to assume that its definition might be extended so it can aggressively apply it when encounter one.

Adding type-level natural numbers

type family (n :: Nat) :+: (m :: Nat) :: Nat   -- uses TypeOperators,
                                               --      TypeFamilies
type instance Zero    :+: m = m
type instance (Suc n) :+: m = Suc (n :+: m)

We can complete the definition for append as follows

append :: Vector a n -> Vector a m -> Vector a (n :+: m)
append (x :- xs) ys = x :- append xs ys
append Nil       ys = ys

Data kinds and type-classes

The point of having the Vector a n as a type is to rule out invalid accesses to its elements at compile time.

Recall the example we started with.
```
> [1,2,3] !! 5
*** Exception: Prelude.(!!): index too large 
```
What should it be the type of index if used on elements of type Vector a n?

In an ideal world, it would be as follows.
```
index :: LessEq n m => (n :: Nat) -> Vector a (Suc m :: Nat) -> a 
```
(We explain below by Suc m instead of m.)

Unfortunately, this type is not a valid type in Haskell. There are many problems with it.

First, we cannot use data kinds to build function types. Recall that (->) :: * -> * -> *, so (n :: Nat) -> .. is ill-typed since n has kind Nat and not *.

We remove n :: Nat from the ideal type.
```
index :: LessEq n m => ...n... -> Vector a (Suc m :: Nat) -> a 
```
Observe that we still need n since it is used by the the type class LessEq n m.

Constraint LessEq n m holds when the type-level natural n is less or equal than m.
```
index :: LessEq n m => ...n... -> Vector a (Suc m :: Nat) -> a 
```
If we consider array (see its definition above) of size Suc (Suc Zero), then n can be either Zero or Suc Zero. Recall that indexes start from 0 for accessing elements in lists by using (!!) -- that is why we have Suc m in the type rather than just m.
We define this type-class in the usual way, but using data kinds.
```
class Less (n :: Nat) (m :: Nat) where  -- uses MultiParamTypeClasses 
```
First, we declare that the Zero type is less or equal than any other type-level natural.
```
instance Less (Zero :: Nat)  m where    -- uses FlexibleInstances  
```
Then, we define the case for non-zero type-level naturals.
```
instance Less n m => Less (Suc n :: Nat) (Suc m :: Nat) where 
```
Observe that the type-classes are empty (i.e., they contain no methods).

Forgetting types

Let us consider what happens when we try to implement index
```
index :: Less n m => ...n... -> Vector a (Suc m :: Nat) -> a
index tn vec = ... !! ... 
```
We want to use (!!) from lists. So, we need to "cast" a vector into a list. This is usually not a problem; after all, forgetting types is not difficult.
```
toList :: Vector a n -> [a]
toList Nil       = []
toList (x :- xs) = x:toList xs 
```
We can then complete the definition of index a little bit more.
```
index :: Less n m => ...n... -> Vector a (Suc m :: Nat) -> a
index tn vec = (toList vec) !! ... 
```

Singleton types

code

In the implementation of index, the second argument for (!!) depends on the type of tn.

For instance, if n has type Zero, the argument needs to be 0. Instead, if n has type Suc (Zero), then the argument needs to be 1.

In other words, for any type-level n, there should be a term-level representation for it. This correspondence can be established using singleton types.
By definition of data promotion, any type n such that n :: Nat has no inhabitants except undefined. Therefore, it is impossible to establish a one-to-one correspondence between types and term-level representations.
Instead, we declare a new inhabited data type which takes types of kind Nat
```
data SNat (n :: Nat) where
     SZero :: SNat Zero
     SSuc  :: SNat n -> SNat (Suc n) 
```
Observe that for any type SNat (n :: Nat), there exists one term which inhabits such type (besides undefined). For instance, if a term t has type SNat Zero, then t has the form SZero. Similarly, if a term t has type SNat (Suc (Suc Zero)), then t is of the form SSuc (SSuc SZero).
Having the type SNat (n :: Nat), we can write a function which synthesizes a term-level integer based on the type-level n :: Nat
```
toNat :: SNat n -> Int
toNat SZero    = 0
toNat (SSuc n) = 1 + toNat n 
```

Using function toNat, we can complete the implementation of index

index :: Less n m => SNat n -> Vector a (Suc m :: Nat) -> a
index tn vec = (toList vec) !! (toNat tn)

Examples

Let us define some indexes of type SNat (n :: Nat) for some type-level index n.

zero = SZero
one  = SSuc SZero
two  = SSuc (SSuc SZero)

Accessing valid indexes in arrays type-checks!

> index zero array
2
> index one array
1
> index two array
     No instance for (Less ('Suc 'Zero) 'Zero)
     ...

Summary

Typing more well-behaved programs
- Associated types
  - Typing more well-behaved programs
  - Used with type-classes
  - It is a type level functions (i.e., type family)
Typing less bad-behaved programs
- Kinds
  - The "type" of types
  - Data kinds (lifting data types and their elements "one level up")
- Type families
  - Type-level functions
- Singleton types