Type-based modeling

Design of DSLs

In our DSLs, we have tree important components: constructors, combinators, and run functions
Sometimes, the DSL type-signature for combinators might allow to construct objects such that have no semantics
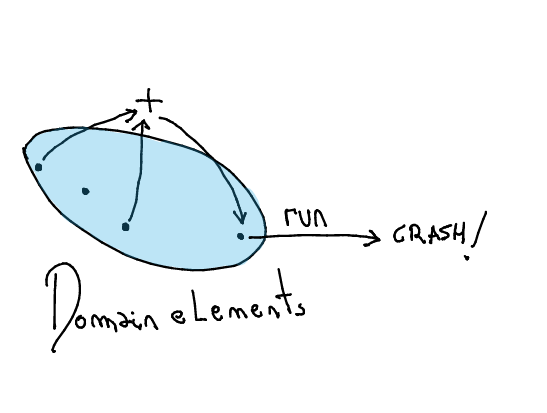
As a result, run functions need to dynamically check that objects "make sense" before running them

A simple (non-monadic) DSL for integers and booleans expressions

The DSL

-- Type of objects
data Expr

-- Constructors
int  :: Int  -> Expr
bool :: Bool -> Expr

-- Combinators
plus  :: Expr -> Expr -> Expr
equal :: Expr -> Expr -> Expr
if    :: Expr -> Expr -> Expr -> Expr

-- Run
type Value

eval :: Expr -> Value

Observe from the interface that the combinators can compose elements of different nature, which might trigger errors in the run function

What is the semantics of the following expressions?
```
ifc (lit 3) (lit 42) (bool False)
```
```
eqc (lit 3) (bool True)
```
The DSL allows to build both well- and ill-typed expressions!
We can start given a complex (and arguably wrong) semantics to bad expressions (JavaScript does that!), e.g., 1 + True == 1, etc.

We assume that ill-typed expressions have no semantics!

Therefore, the run function needs to trigger errors when expressions are bad.

An EDSL implementation

code

We implement Expr as follows

data Expr where
  LitI   :: Int  -> Expr
  LitB   :: Bool -> Expr
  (:+:)  :: Expr -> Expr -> Expr
  (:==:) :: Expr -> Expr -> Expr
  If     :: Expr -> Expr -> Expr -> Expr

The interesting case is the run function

eval :: Expr -> Value

Since expressions can be reduced to integers or booleans, an element of type Value is either an integer or a boolean.

data Value = VInt Int | VBool Bool

The run function then checks that expressions are evaluated to the expected type of values at every combinator.

eval :: Expr -> Value
eval (LitI n)       =  VInt n
eval (LitB b)       =  VBool b
eval (e1 :+: e2)     =  plus (eval e1) (eval e2)
  where plus (VInt n) (VInt m) = VInt $ n + m
        plus _        _        = error "plus: type error"
eval (e1 :==: e2)    =  eq (eval e1) (eval e2)
  where eq (VInt n)  (VInt m)  = VBool $ n == m
        eq (VBool a) (VBool b) = VBool $ a == b
        eq _         _         = error "equal: type error"
eval (If e1 e2 e3)  =  case eval e1 of
  VBool True   -> eval e2
  VBool False  -> eval e3
  _            -> error "if: type error"

Ill-typed expressions raise errors when evaluating them

eBad2 = If (LitI 20) (LitI 1) (LitI 7)

> eval eBad2
*** Exception: if: type error!

The picture

Can we avoid constructing bad expressions at all?

A EDSL with type-aware combinators

code

Now, for every type, we have a new kind of expressions

data ExprI  -- Integer expressions
data ExprB  -- Boolean expressions

Combinators can be defined on the right "kind of expressions"

(:+:) :: ExprI -> ExprI -> ExprI
If    :: ExprB -> ExprI -> ExprI -> ExprI

While this looks attractive, and indeed helps, it requires to introduce many new constructors to deal with all the possible "good" ways to build expressions.

data ExprI where
  LitI  :: Int -> ExprI
  (:+:) :: ExprI -> ExprI -> ExprI
  IfI   :: ExprB -> ExprI -> ExprI -> ExprI

data ExprB where
  LitB :: Bool -> ExprB
  EqI  :: ExprI -> ExprI -> ExprB
  EqB  :: ExprB -> ExprB -> ExprB
  IfB  :: ExprB -> ExprB -> ExprB -> ExprB

Observe the reproduction of equality constructors (EqI and EqB) and branches (IfI and IfB) depending on the type of arguments they take.

There are two run functions, one for each type of expressions

evalI :: ExprI -> Int
evalI (LitI n)    = n
evalI (e1 :+: e2) = evalI e1  +  evalI e2
evalI (IfI b t e) = if evalB b then evalI t else evalI e

evalB :: ExprB -> Bool
evalB (LitB b)    = b
evalB (EqI e1 e2) = evalI e1  ==  evalI e2
evalB (EqB e1 e2) = evalB e1  ==  evalB e2
evalB (IfB b t e) = if evalB b then evalB t else evalB e

Observe that evalI and evalB do not raise type-errors.

We can use this EDSL to validate a value of type Expr
In other words, we take a value of type Expr and map it into either ExprI or ExprB.

If successful, we can run a value of type Expr using evalA or evalB, so no type errors!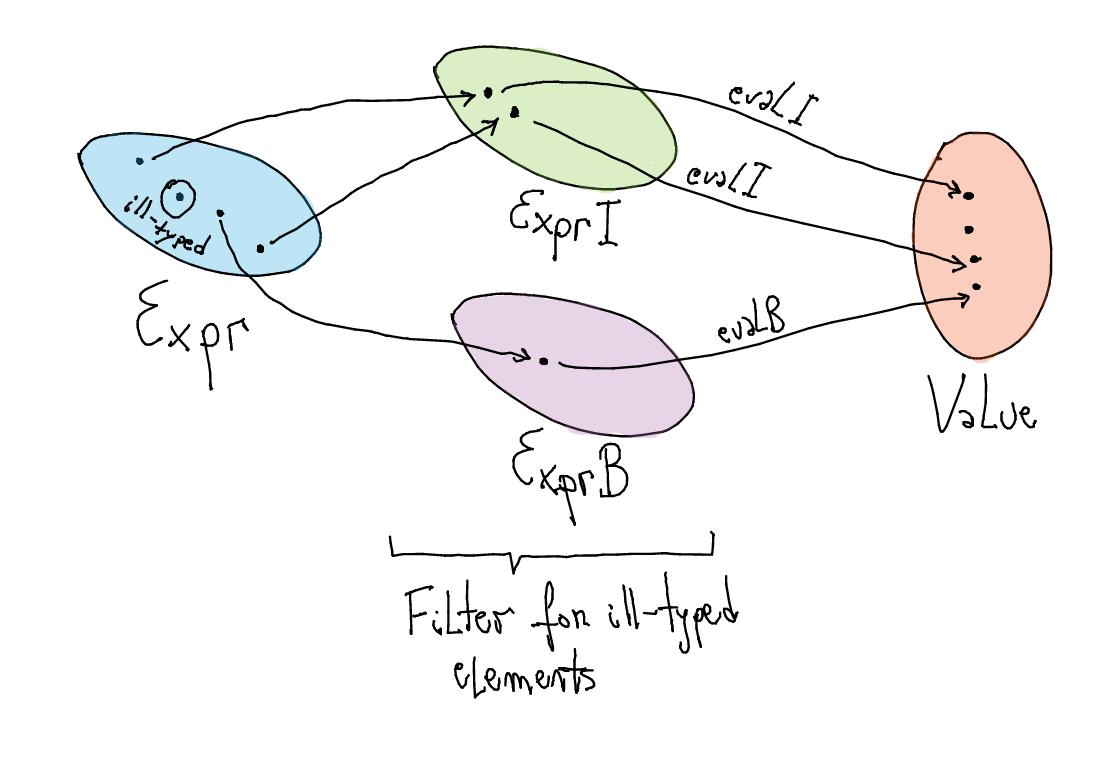

We need to write a function which infers the type for a value of type Expr

infer :: Expr -> ?

There are three possible outcomes for infer e, i.e., it might produce an error (e has no type) or either a value of type ExprI or ExprB.

import qualified Expr as E

data TypedExpr = TInt ExprI | TBool ExprB

infer :: E.Expr -> Maybe TypedExpr

The easy cases are the constructors.

infer (E.LitB b)    = return $ TBool (LitB b)
infer (E.LitI i)    = return $ TInt  (LitI i)

For addition, we need both argument to be integer expressions.

infer (e1 E.:+: e2)  = do
 te1 <- infer e1
 te2 <- infer e2
 inferPlus te1 te2

Function inferPlus checks that both te1 :: TypedExpr and te2 :: TypedExpr are integers and, if that is the case, it constructs the corresponding value of type ExprI, i.e., a sum.

inferPlus :: TypedExpr -> TypedExpr -> Maybe TypedExpr
inferPlus (TInt e1) (TInt e2) = Just (TInt (e1 :+: e2))
inferPlus _         _         = Nothing

In a similar manner, we write the cases for equality and branches.

infer (e1 E.:==: e2) = do
  te1 <- infer e1
  te2 <- infer e2
  inferEq te1 te2
infer (E.If b t e)  = do
  tb <- infer b
  tt <- infer t
  te <- infer e
  inferIf tb tt te

**Exercise**: write `inferEq` and `inferIf`

We write eval only for typed expressions so we guarantee no type errors

eval :: TypedExpr -> E.Value
eval (TInt  ei) = E.VInt  $ evalI ei
eval (TBool eb) = E.VBool $ evalB eb

Problems with this approach:

Duplication of constructors to denote "the same operation" but on different type of expressions

It does not scale up for type constructors (e.g., lists, tuples, monads, etc.)

For instance, if we want to introduce lists, we need to define a type for list expressions

List of integers.

data ExprLI where
     EmptyLI :: ExprLI
     ConsLI  :: ExprI  -> ExprLI -> ExprLI

data ExprB where
     ...
     EqLI :: ExprLI -> ExprLI -> ExprB

List of booleans.

data ExprLB where
     EmptyLB :: ExprLB
     ConsLB  :: ExprB  -> ExprLB -> ExprLB

data ExprB where
     ...
     EqLI :: ExprLI -> ExprLI -> ExprB
     EqLB :: ExprLB -> ExprLB -> ExprB

What about having lists of lists?

List of lists of integers.

data ExprLLI where
     EmptyLLI :: ExprLLI
     ConsLLI  :: ExprLI  -> ExprLLI -> ExprLLI

data ExprB where
     ...
     EqLI  :: ExprLI -> ExprLI -> ExprB
     EqLB  :: ExprLB -> ExprLB -> ExprB
     EqLLI :: ExprLLI -> ExprLLI -> ExprB

List of lists of booleans.

data ExprLLB where
     EmptyLLB :: ExprLLB
     ConsLLB  :: ExprLB  -> ExprLLB -> ExprLLB

data ExprB where
     ...
     EqLI  :: ExprLI -> ExprLI -> ExprB
     EqLB  :: ExprLB -> ExprLB -> ExprB
     EqLLI :: ExprLLI -> ExprLLI -> ExprB
     EqLLB :: ExprLLB -> ExprLLB -> ExprB

What about lists of lists of lists of integers/booleans?

Enter GADTs

code

We use GADTs of the form Expr t, where t is a Haksell type which indicates the value that the expression denotes
```
data Expr t where
  LitI   :: Int -> Expr Int
  LitB   :: Bool -> Expr Bool
  (:+:)  :: Expr Int -> Expr Int -> Expr Int
  (:==:) :: Eq t => Expr t -> Expr t -> Expr Bool
  If     :: Expr Bool -> Expr t -> Expr t -> Expr t 
```
Observe constructors LitI and LitB produce integer and boolean expressions, respectively. The combinator (:+:) takes integer expressions, i.e., arguments of type Expr Int, and produces an integer expression as well. Equality of expressions of type Expr t requires that t supports equality in Haskell -- see the type constraint Eq t. Constructor If takes a boolean expression as the guard (Expr Bool) and both branches need to return the same type of expressions (Expr t).

There is no way to construct ill-typed expression in `Expr t`

The run function is simply defined as follows.

eval :: Expr t -> t
eval (LitI n)     = n
eval (LitB b)     = b
eval (e1 :+: e2)  = eval e1 +  eval e2
eval (e1 :==: e2) = eval e1 == eval e2
eval (If b t e)   = if eval b then eval t else eval e

We can forget that an expression is typed

To go from typed expressions to untyped ones is easy! (type elimination)

To go from untyped expressions to typed ones is not straightforward! (type inference)

Type elimination

forget :: Expr t -> E.Expr
forget e = case e of
  LitI n      -> E.LitI n
  LitB b      -> E.LitB b
  e1 :+: e2   -> forget e1 E.:+:  forget e2
  e1 :==: e2  -> forget e1 E.:==: forget e2
  If e1 e2 e3 -> E.If (forget e1) (forget e2) (forget e3)

By doing so, we can reuse the pretty printing for the untyped version of Expr
```
instance Show (Expr t) where
  showsPrec p e = showsPrec p (forget e) 
```
Type inference is a bit more involved

If e is an expression which produces a boolen, then
```
infer e :: Maybe (Expr Bool) 
```
If e is an expression which produces an integer, then
```
infer e :: Maybe (Expr Int) 
```
So, what is the type signature for infer?
```
infer :: E.Expr -> Maybe ? 
```
The returning type depends on the (value of the) argument of the function!
Challenge

Our inference function will have to convince the Haskell type checker to allow us to construct an element of `Expr t` from an untyped expression `E.Expr`.

Existential types

When the returning type of a function depends on the (value of the) argument of a function, we can use existential types to make them type-check
```
data TypedExpr where
     (:::) :: forall t. Eq t => Expr t -> TypedExpr 
```
It is counter intuitive to use forall t to express an existential type. The contructor (:::) can be instantiated with any type t which supports equality.

Observe that type t does not show up in the data type declaration TypedExpr. If we have a value d :: TypedExpr, we know that it is built with the constructor (:::). Observe, however, we cannot guess which type t has been used, thus we only know that there exists a type t (with equality) which builds d!
Typing infer
```
infer :: E.Expr -> Maybe TypedExpr 
```
We add more information to the constructor (:::) to include not only the expression but its type as well
```
data Type t where
  TInt  :: Type Int
  TBool :: Type Bool

data TypedExpr where
  (:::) :: forall t. Eq t => Expr t -> Type t -> TypedExpr 
```
Observe that (e ::: te) :: TypedExpr indicates that expression e :: Expr t has type te :: Type t.
Observe that types Type Int and Type Bool have only one inhabitant, respectively (we exclude undefined).

This kind of types are known as singleton types. Why is it useful?

Singleton types

There is a one-to-one correspondence between terms and types

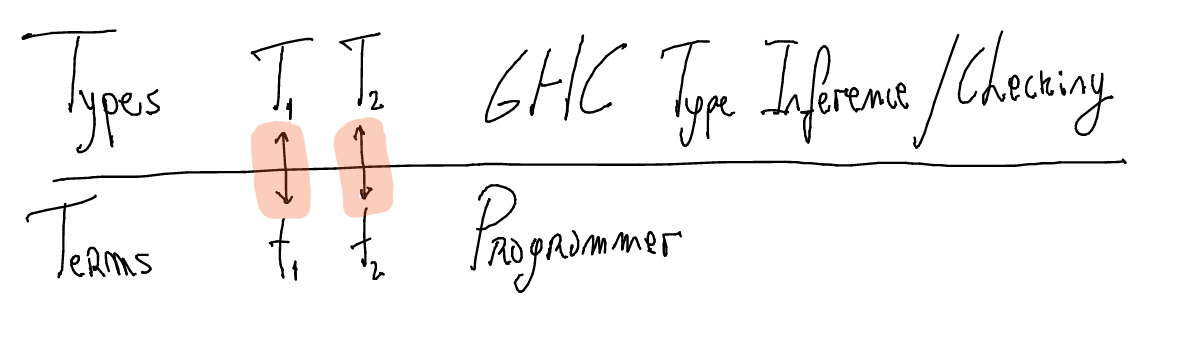
This correspondence is useful to guide Haskell's type-system by coding using the singleton's types inhabitants.
In our example, function infer is going to use them to indicate that (i) expressions are either typed as Expr Int or Expr Bool, and (ii) some expressions should have the same type.

Implementing type inference

We start by defining a mechanisms to tell Haskell that two types must be the same.
```
data Equal a b where
  Refl :: Equal a a 
```
Equal a b is a type of proofs that two types a and b are equal. The only way to prove two types equal is if they are in fact the same, and then the proof is Refl.

Evaluating one of these proofs to Refl will convince GHC's type checker that the two type arguments are indeed equal (how else could the proof be Refl?).

For instance, if we have a proof p :: Equal Int Int, then we know that p is Refl since Refl :: Equal Int Int and it is the only inhabitant for that type.

On the other hand, p :: Equal Int Float cannot be constructed. Do you see why? The type Equal Int Float has no inhabitant, i.e., there is no constructor to build it (Refl does not work for this case).
We construct a function which takes two types for expressions and hints Haskell if they have the same type
```
(=?=) :: Type s -> Type t -> Maybe (Equal s t) 
```
This function will only succeed when type s is equal to type t.

How are we going to indicate that in the body of the function? After all, functions implementations do not talk about types!

We have singleton types, so we can use their inhabitants to refer to types from the function body.
```
(=?=) :: Type s -> Type t -> Maybe (Equal s t)
TInt  =?= TInt  = Just Refl
TBool =?= TBool = Just Refl
_     =?= _     = Nothing   
```
In the infer function, we can make heavy use of the fact that pattern matching on a Type t or an Equal s t will tell GHC's type checker interesting things about s and t
Inferring types for constructors
```
 infer :: E.Expr -> Maybe TypedExpr
 infer e = case e of
   E.LitI n -> return (LitI n ::: TInt)
   E.LitB b -> return (LitB b ::: TBool) 
```
Because the use of LitI (LitB), GHC knows that LitI n :: Expr Int (LitB b :: TBool), and consequently has type Type Int. Consequently, we could have place undefined instead of TInt (TBool) -- after all, GHC's type system already knows everything -- and infer will still type checks. However, it might produce infer to crash later on (see other cases)
Inferring types for addition
```
infer :: E.Expr -> Maybe TypedExpr
infer e = case e of
  ...
  r1 E.:+: r2 -> do
    e1 ::: TInt  <-  infer r1
    e2 ::: TInt  <-  infer r2
    return (e1 :+: e2 ::: TInt) 
```
By doing pattern-matching using TInt (i.e., e1 ::: TInt and e2 ::: TInt), we are telling GHC that infer r1 :: Maybe TypedExpr and infer r2 :: Maybe TypedExpr needs to construct integer expressions e1 :: Expr Int and e2 :: Expr Int, respectively.

Inferring types for equality

This case is interesting.

infer :: E.Expr -> Maybe TypedExpr
infer e = case e of
  ...
  r1 E.:==: r2 -> do
    e1 ::: t1    <-  infer r1
    e2 ::: t2    <-  infer r2
    ...
    return (e1 :==: e2 ::: TBool)

We know that the result is something of type Expr Bool. We indicate by using (:===:) and TBool in the returned value.

However, the expressions e1 and e2 might have any type (e.g., Expr Int, or Expr Bool) as long as they are the same. We hint that to GHC's type system by using function (=?=) and pattern-matching on its result.

infer :: E.Expr -> Maybe TypedExpr
infer e = case e of
  ...
  r1 E.:==: r2 -> do
    e1 ::: t1    <-  infer r1
    e2 ::: t2    <-  infer r2
    Refl         <-  t1 =?= t2
    return (e1 :==: e2 ::: TBool)

Inferring types for branches

We hint GHC that the guard needs to be boolean (by applying pattern-matching), and that the branches have the same type (by applying function (=?=) and pattern-matching on its result).

infer :: E.Expr -> Maybe TypedExpr
infer e = case e of
  ...
  E.If r1 r2 r3 -> do
    e1 ::: TBool <-  infer r1
    e2 ::: t2    <-  infer r2
    e3 ::: t3    <-  infer r3
    Refl         <-  t2 =?= t3
    return (If e1 e2 e3 ::: t2)

Type checking and evaluation

We can do type checking by inferring a type and comparing it to the type we expect.

check :: E.Expr -> Type t -> Maybe (Expr t)
check r t = do
  e ::: t' <- infer r
  Refl     <- t' =?= t
  return e

Evaluation

As we did before, we first type-check an expression and then run it.
```
evalT :: E.Expr -> Maybe E.Value 
```
Recall that E.Value has the constructors VBool Bool and VInt Int.

In this light, if an expression E.Expr has type Type Int, then evalT should return VInt n (for some n).
```
evalTI :: E.Expr -> Maybe E.Value
evalTI e = do
  i <- check e TInt
  return (E.VInt $ eval i) 
```
Observe the use of TInt to hint GHC's type system.

Similarly, we have a function for expression with type Type Bool.
```
evalTB :: E.Expr -> Maybe E.Value
evalTB e = do
  b <- check e TBool
  return (E.VBool $ eval b) 
```
Observe that we are calling eval from our original approach (the one that might report type-errors). However, this function is not going to raise any of them!

Function evalT simply tries to type expressions as Type Bool or Type Int and returns the appropriated value.
```
evalT :: E.Expr -> Maybe E.Value
evalT e = evalTB e  `mplus`  evalTI e 
```

Summary

Adding type-inference / type-checking to DSLs
- Avoid constructing semantically bad entities
- No type-errors reported by the run function
GADTs
- It allows to express some invariants about how constructors and combinators should work (e.g., the guard of a branch is a boolean expression)
We verify that entities built with the DSL interface are well-typed, i.e., they accommodate to the GADTs invariants
- We implement type-inference for the elements built with the DSL interface
- We use existential types to give a type to the inference function
- We use singleton types to hint GHC's type-system about the expected types for the GADTs elements
- We use a proof of equality to hint GHC's type-system when two GADTs values should have the same type.